Exercise 10.5 class 9 solutions || circles class 9 exercise 10.5 || class 9 maths chapter 10 exercise 10.5 || class 9 exercise 10.5 || exercise 10.5 class 9 || class 9 circles exercise 10.5 || exercise 10.5 class 9 maths || ncert solutions for class 9 chapter circles exercise 10.5
Discover step-by-step solutions for Class 9 Maths Chapter 10, Exercise 10.5, which takes students further into the fascinating world of circle geometry by introducing tangents and their unique properties. This exercise emphasizes how tangents behave in relation to circles—particularly how a tangent to a circle is always perpendicular to the radius at the point of contact. Students explore key theorems involving tangents from external points, uncovering symmetrical properties and proving that tangents drawn from the same external point are equal in length. The use of visual aids and guided reasoning in Exercise 10.5 helps students gain confidence in tackling proof-based questions, enhancing both their problem-solving abilities and their appreciation of the mathematical beauty hidden within circles.
exercise 10.5 class 9 solutions || circles class 9 exercise 10.5 || class 9 maths chapter 10 exercise 10.5 || class 9 exercise 10.5 || exercise 10.5 class 9 || class 9 circles exercise 10.5 || exercise 10.5 class 9 maths || ncert solutions for class 9 chapter circles exercise 10.5
Exercise 10.5
1. In Fig. 10.36, A, B and C are three points on a circle with
centre \( O \) such that \( \angle B O C=30^{\circ} \) and \(
\angle A O B=60^{\circ} \). If \( D \) is a point on the circle
other than the arc \(ABC \), find \( \angle {ADC} \).
Answer
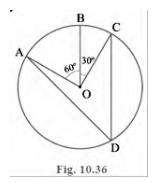
\(\angle {AOC}=\angle {AOB}+\angle {BOC}\)\(=60^{\circ}+30^{\circ}\)
\(=90^{\circ}\)
We know that angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining part of the circle
\(\angle {ADC}=\frac{1}{2} \angle {AOC}\)
\(=\frac{1}{2} \times 90^{\circ}\)
\(=45^{\circ}\)
2. A chord of a circle is equal to the radius of the circle. Find
the angle subtended by the chord at a point on the minor arc and
also at a point on the major arc.
Answer
In \( \triangle {OAB} \),
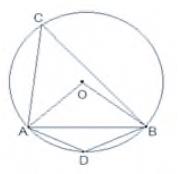
\( {AB}={OA}={OB}= \) Radius
\( \triangle {OAB} \) is an equilateral triangle
Therefore, each interior angle of this triangle will be of \( 60^{\circ} \)
\(\angle {AOB}=60^{\circ}\)
\(\angle {ACB}=\frac{1}{2} \times {AOB}\)
\(=\frac{1}{2} \times 60^{\circ}\)
\(=30^{\circ}\)
In cyclic quadrilateral \( A C B D \)
\(\angle {ACB}+\angle {ADB}=180^{\circ}(\text {Opposite angle in cyclic quadrilateral})\)
\(\angle {ADB}=180^{\circ}-30^{\circ}\)
\(=150^{\circ}\)
Therefore, angle subtended by this chord at a point on the major arc and the minor arc are \( 30^{\circ} \) and \( 150^{\circ} \) respectively
3. In Fig. 10.37, \( \angle {PQR}=100^{\circ} \), where \( {P},
{Q} \) and \(R\) are points on a circle with centre \(O\). Find \(
\angle {OPR} \).
Answer
Method 1:
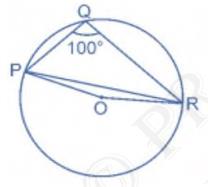
We know angle subtended at centre by an arc is double the angle subtended by it at any other point.
Reflex angle \( \angle {POR}=2 \angle {PQR} \)
\(=2 \times 100^{\circ}\)
\(=200^{\circ}\)
Now, \( \angle {POR}=360^{\circ}-200=160^{\circ} \)
Also,
\( {PO}={OR} \quad\) [Radii of a circle]
\( \angle {OPR}=\angle {ORP}\quad \) [Opposite angles of isosceles triangle]
In \( \triangle {OPR}, \angle {POR}=160^{\circ} \)
\( \therefore \angle {OPR}=\angle {ORP}=10^{\circ} \)
Method 2:
Consider \(PR\) as a chord of the circle. Take any point \( S \) on the major arc of the circle
\(PQRS\) is a cyclic quadrilateral
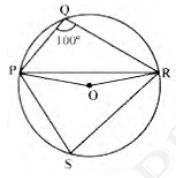
\(\angle {PQR}+\angle {PSR}=180^{\circ}\) (Opposite angles of a cyclic quadrilateral)
\(\angle {PSR}=180^{\circ}-100^{\circ}=80^{\circ}\)
We know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle
\(\angle {POR} =2 \angle {PSR}\)
\(=2\left(80^{\circ}\right)\)
\(=160^{\circ}\)
In \( \triangle {POR} \),
\( {OP}={OR} \quad \) (Radii of the same circle)
\( \angle {OPR}=\angle {ORP} \) (Angles opposite to equal sides of a triangle)
\(\angle {OPR}+\angle {ORP}+\angle {POR}=180^{\circ}(\text {Angle sum property of a triangle})\)
\(\angle {OPR}+160^{\circ}=180^{\circ}\)
\(2 \angle {OPR}=180^{\circ}-160^{\circ}\)
\(2 \angle {OPR}=20^{\circ}\)
\(\angle {OPR}=10^{\circ}\)
4. In Fig. 10.38, \( \angle {ABC}=69^{\circ}, \angle
{ACB}=31^{\circ} \), find \( \angle {BDC} \).
Answer
\(\angle {BAC}=\angle {BDC}\) (Angles in the segment of the
circle)In triangle \(ABC \),
\(\angle {BAC}+\angle {ABC}+\angle {ACB}=180^{\circ}(\text {Sum of all angles in a triangle})\)
\(\angle {BAC}+69^{\circ}+31^{\circ}=180^{\circ}\)
\(\angle {BAC}=180^{\circ}-100^{\circ}\)
\(\angle {BAC}=80^{\circ}\)
Thus,
\(\angle {BDC}=80^{\circ}\)
exercise 10.5 class 9 solutions || circles class 9 exercise 10.5 || class 9 maths chapter 10 exercise 10.5 || class 9 exercise 10.5 || exercise 10.5 class 9 || class 9 circles exercise 10.5 || exercise 10.5 class 9 maths || ncert solutions for class 9 chapter circles exercise 10.5
5. In Fig. 10.39, \(A, B, C\) and \(D\) are four points on a
circle. \(AC\) and \(BD\) intersect at a point \(E\) such that \(
\angle {BEC}=130^{\circ} \) and \( \angle {ECD}=20^{\circ} \).
Find \( \angle BAC\).
Answer
In \( \triangle {CDE} \),\(\angle {CDE}+\angle {DCE}={CEB} \text { (Exterior angle) }\)
\(\angle {CDE}+20^{\circ}=130^{\circ}\)
\(\angle {CDE}=110^{\circ}\)
However, \( \angle {BAC}=\angle {CDE} \) (Angles in the same segment of a circle)
\(\angle B A C=110^{\circ}\)
As angles in same segment are equal. So,
\(\angle B A C=\angle B D C=110^{\circ}\)
6. \( ABCD\) is a cyclic quadrilateral whose diagonals intersect
at a point \( E \). If \( \angle D B C=70^{\circ}, \angle B A C \)
is \( 30^{\circ} \), find \( \angle B C D \). Further, if \( A B=
\) \( B C \), find \( \angle E C D \).
Answer
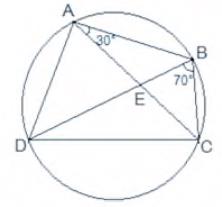
METHOD 1:
For chord \(CD\),
\( \angle {CBD}=\angle {CAD} \) (Angles on the same segment are equal)
\(\angle {CAD} =70^{\circ}\)
\(\angle {BAD} =\angle {BAC}+\angle {CAD}\)
\( =30^{\circ}+70^{\circ}\)
\(=100^{\circ}\)
\( \angle {BCD}+\angle {BAD}=180^{\circ} \) (Opposite angles of a cyclic quadrilateral)
\(\angle {BCD}+100^{\circ} =180^{\circ}\)
\(\angle {BCD} =80^{\circ}\)
Now, In \( \triangle {ABC} \),
\({AB} ={BC}\) (Given)
\(\angle {BCA} =\angle {CAB}\) (Angles opposite to equal sides of a triangle)
\(\angle {BCA} =30^{\circ}\)
We have,
\(\angle {BCD}=80^{\circ}\)
\(\angle {BCA}+\angle {ACD}=80^{\circ}\)
\(30^{\circ}+\angle {ACD}=80^{\circ}\)
\(\angle {ACD}=50^{\circ}\)
As \( \angle {ACD}=\angle {ECD} \)
\( \angle E C D=50^{\circ} \)
METHOD 2:
On chord \(AD\),
\( \angle {ABD}=\angle {ECD}\quad \ldots\ldots\text{(1)} \) [Since angles on the same segment are equal]
In \( \triangle {ABC} \),
Given: \( {AB}={BC} \) Therefore, \( \angle {BAC}=\angle {BCA}=30^{\circ} \)
Sum of angles of a triangle \( =180^{\circ} 30^{\circ}+30^{\circ}+\angle A B C=180^{\circ} \)
\( \angle {ABC}=120^{\circ}\quad \ldots\ldots\text{(2)} \)
And we can see that
\(\angle {ABC}=\angle {ABD}+\angle {DBC} 120^{\circ}=\angle {ABD}+70^{\circ} \angle {ABD}=50^{\circ}\)
And from equation \(1\), we can see that,
\(\angle {ECD}=50^{\circ}\)
7. If diagonals of a cyclic quadrilateral are diameters of the
circle through the vertices of the quadrilateral, prove that it is
a rectangle.
Answer
Let ABCD be a cyclic quadrilateral having diagonals BD and AC,
intersecting each other at point O. 
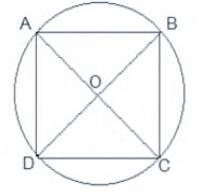
\( {n} \triangle {AOD} \) and \( \triangle {COB} \)
\({AO}={CO}\quad {[\text {Radii of a circle}] }\)
\({OD}={OB}\quad {[\text {Radii of a circle}] }\)
\(\angle {AOD}=\angle {COB} \quad{[\text {Vertically opposite angles}] }\)
\(\therefore \triangle {AOD} \cong \triangle {COB} \quad{[\text {SAS congruency}] }\)
\(\therefore \angle {OAD}=\angle {OCB} \quad{[{CPCT}] }\)
But these are alternate interior angles made by the transversal AC, intersecting AD and BC.
\( \therefore {AD} \| {BC} \)
Similarly, \( {AB} \| {CD} \).
Hence, quadrilateral ABCD is a parallelogram.
Also, \( \angle {ABC}=\angle {ADC} \quad \ldots\ldots\text{(i)}\) [Opposite angles of a \( \| {gm} \) is equal]
And, \( \angle {ABC}+\angle {ADC}=180^{\circ} \quad \ldots\ldots\text{(ii)}\) [Sum of opposite angles of a cyclic quadrilateral is \( 180^{\circ} \)]
\( \Rightarrow \angle {ABC}=\angle {ADC}=90^{\circ} \quad\) [From (i) and (ii)]
\( \therefore {ABCD} \) is a rectangle.
[A \(\|\text{gm}\) one of whose angles are \( 90^{\circ} \) is a rectangle]
Hence Proved.
exercise 10.5 class 9 solutions || circles class 9 exercise 10.5 || class 9 maths chapter 10 exercise 10.5 || class 9 exercise 10.5 || exercise 10.5 class 9 || class 9 circles exercise 10.5 || exercise 10.5 class 9 maths || ncert solutions for class 9 chapter circles exercise 10.5
8. If the non-parallel sides of a trapezium are equal, prove that
it is cyclic.
Answer
Consider a trapezium ABCD with\( {AB} \| {CD} \) and
\({BC}={AD}\)
Draw AM perpendicular to \( C D \) and \( B N \) perpendicular to \( C D \)
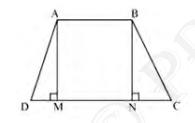
In \( \triangle {AMD} \) and \( \triangle {BNC} \),
\({AD} ={BC}\) (Given)
\(\angle {AMD} =\angle {BNC}\) (By construction, each is \( 90^{\circ} \))
\({AM} ={BN}\) (Perpendicular distance between two parallel lines is same)
\(\triangle {AMD} \cong \triangle {BNC} \ (\text {RHS congruence rule})\)
\(\angle {ADM}=\angle {BCN} \ ({CPCT})\)
\(\Rightarrow \angle {ADC}=\angle {BCD}\quad \ldots\ldots\text{(i)}\)
\(BAD\) and \(ADC\) are on the same side of transversal \(AD\)
\( \angle {BAD}+\angle {ADC}=180^{\circ} \quad \ldots\ldots\text{(ii)}\)
\( \angle {BAD}+\angle {BCD}=180^{\circ} \) [Using equation (i)]
This equation shows that the opposite angles are supplementary
Therefore, ABCD is a cyclic quadrilateral.
9. Two circles intersect at two points \(B\) and \(C\). Through
\(B\), two line segments \( A B D \) and \( P B Q \) are drawn to
intersect the circles at \( A, D \) and \(P , Q\) respectively
(see Fig. 10.40). Prove that \( \angle {ACP}=\angle {QCD} \)
Answer
Join chords AP and DQ
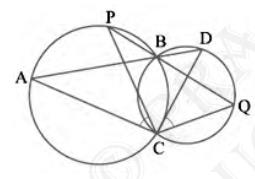
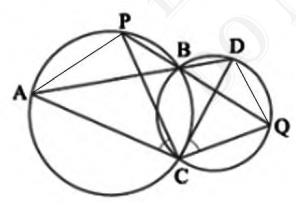
For chord AP,
\( \angle {PBA}=\angle {ACP} \) (Angles in the same segment) \(\quad \ldots\ldots\text{(i)}\)
For chord DQ,
\( \angle {DBQ}=\angle {QCD} \) (Angles in the same segment) \(\quad \ldots\ldots\text{(ii)}\)
\( A B D \) and \( P B Q \) are line segments intersecting at \( B \)
\( \angle {PBA}=\angle {DBQ} \quad \) (Vertically opposite angles) \(\quad \ldots\ldots\text{(iii)}\)
From (i), (ii), and (iii), we get
\( \angle {ACP}=\angle {QCD} \)
hence proved
10. If circles are drawn taking two sides of a triangle as
diameters, prove that the point of intersection of these circles
lie on the third side.
Answer
Consider a \( \triangle {ABC} \)Two circles are drawn while taking AB and AC as the diameter Join AD
\( \angle {ADB}=90^{\circ} \quad \) (Angle subtended by semi-circle)
\( \angle {ADC}=90^{\circ} \quad \) (Angle subtended by semi-circle)
\( \angle {BDC}=\angle {ADB}+\angle {ADC}=90^{\circ}+90^{\circ}=180^{\circ} \)
Therefore, BDC is a straight line
Thus, Point D lies on the third side BC of \( \triangle {ABC} \).
11. ABC and ADC are two right triangles with common hypotenuse
AC. Prove that \( \angle {CAD}=\angle {CBD} \)
Answer
It is given in the question that,AC is the common hypotenuse
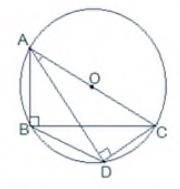
So, \( \angle B=\angle D=90^{\circ} \)
We have to prove that,
\(\angle C A D=\angle C B D\)
Proof: We know that,
\( \angle {ABC} \) and \( \angle {ADC} \) are \( 90^{\circ} \) as these angles are in a circle
Thus, both the triangles are lying in the circle and both have same diameter i.e. AC
Points A, B, C and D are noncyclic
Therefore, CD is the chord
So,
\( \angle {CAD}=\angle {CBD} \) (As, angles made by a chord in the same segment are equal)
12. Prove that a cyclic parallelogram is a rectangle.
Answer
Given that: \(ABCD\) is a cyclic quadrilateral 
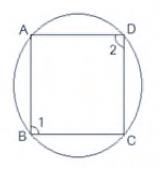
We have to prove that: \( A B C D \) is a rectangle
Proof: \( \angle 1+\angle 2=180^{\circ} \) (Sum of opposite angles of a cyclic parallelogram)
We also know that, opposite angles of a cyclic parallelogram are equal
Therefore,
\(\angle 1=\angle 2\)
\(\angle 1+\angle 1=180^{\circ}\)
\(\angle 1=90^{\circ}\)
As,
One of the interior angle of the parallelogram is \( 90^{\circ} \)
Therefore, \(ABCD\) is a rectangle.
