class 9 exercise 11.1 || class 9 maths exercise 11.1 solution || class 9 maths construction exercise 11.1 || exercise 11.1 class 9 || rd sharma class 9 construction || class 9 maths chapter 11 exercise 11.1 || class 9 maths construction exercise 11.1 || ncert maths class 9 chapter 11 solutions || class 9 math exercise 11.1
Explore step-by-step solutions for Class 9 Maths Chapter 11, Exercise 11.1, which introduces students to the practical application of geometrical constructions using ruler and compass. This exercise helps learners develop accuracy and logical thinking by guiding them through problems such as constructing bisectors of angles, perpendiculars from points and triangles under specific conditions. Through these tasks, students enhance their understanding of fundamental geometric principles while improving their drawing precision and visualization skills—skills that are essential for mastering higher-level geometry.

class 9 exercise 11.1 || class 9 maths exercise 11.1 solution || class 9 maths construction exercise 11.1 || exercise 11.1 class 9 || rd sharma class 9 construction || class 9 maths chapter 11 exercise 11.1 || class 9 maths construction exercise 11.1 || ncert maths class 9 chapter 11 solutions || class 9 math exercise 11.1
Exercise 11.1
1. Construct an angle of \( 90^{\circ} \) at the initial point of
a given ray and justify the construction.
Answer
To construct an angle \( 90^{\circ} \), follow the given steps:1. Draw a ray OA
2. Take O as a centre with any radius, draw an arc DCB is that cuts OA at B .
3. With \( B \) as a centre with the same radius, mark a point \( C \) on the arc DCB.
4. With C as a centre and the same radius, mark a point D on the arc DCB.
5. Take C and D as centre, draw two arcs which intersect each other with the same radius at P .
6. Finally, the ray OP is joined which makes an angle \( 90^{\circ} \) with OP is formed.
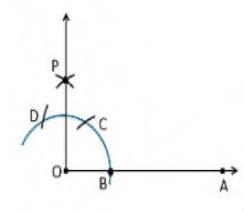
Justification
To prove \( \angle \mathrm{POA}=90^{\circ} \)
In order to prove this, draw a dotted line from the point O to C and O to D and the angles formed are:
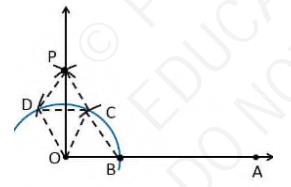
From the construction, it is observed that
\(\mathrm{OB}=\mathrm{BC}=\mathrm{OC}\)
Therefore, OBC is an equilateral triangle
So that, \( \angle \mathrm{BOC}=60^{\circ} \).
Similarly,
\(\mathrm{OD}=\mathrm{DC}=\mathrm{OC}\)
Therefore, DOC is an equilateral triangle
So that, \( \angle D O C=60^{\circ} \).
From SSS triangle congruence rule
\(\triangle \mathrm{OBC} \cong \mathrm{OCD}\)
So, \( \angle \mathrm{BOC}=\angle \mathrm{DOC}[ \) By C.P.C.T \( ] \)
Therefore, \( \angle \mathrm{COP}=\frac{1} {2} \angle \mathrm{DOC}=\frac{1} {2} \left(60^{\circ}\right) \).
\(\angle C O P=30^{\circ}\)
To find the \( \angle \mathrm{POA}=90^{\circ} \) :
\(\angle \mathrm{POA}=\angle \mathrm{BOC}+\angle \mathrm{COP}\)
\(\angle \mathrm{POA}=60^{\circ}+30^{\circ}\)
\(\angle \mathrm{POA}=90^{\circ}\)
Hence, justified.
2. Construct an angle of \( 45^{\circ} \) at the initial point of
a given ray and justify the construction.
Answer
1. Draw a ray OA2. Take O as a centre with any radius, draw an arc DCB is that cuts OA at B.
3. With \( B \) as a centre with the same radius, mark a point C on the arc DCB.
4. With C as a centre and the same radius, mark a point D on the arc DCB.
5. Take C and D as centre, draw two arcs which intersect each other with the same radius at \( P \).
6. Finally, the ray OP is joined which makes an angle \( 90^{\circ} \) with OP is formed.
7. Take B and Q as centre draw the perpendicular bisector which intersects at the point \( R \)
8. Draw a line that joins the point O and R
9. So, the angle formed \( \angle R O A=45^{\circ} \)
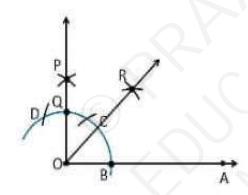
Justification
From the construction,
\(
\angle \mathrm{POA}=90^{\circ}
\)
From the perpendicular bisector from the point B and Q, which divides the \( \angle \) POA into two halves. So it becomes
\( \angle \mathrm{ROA}=\frac{1}{2} \angle \mathrm{POA} \)
\( \angle \mathrm{ROA}=\left(\frac{1}{2}\right) \times 90^{\circ}=45^{\circ} \)
Hence, justified
class 9 exercise 11.1 || class 9 maths exercise 11.1 solution || class 9 maths construction exercise 11.1 || exercise 11.1 class 9 || rd sharma class 9 construction || class 9 maths chapter 11 exercise 11.1 || class 9 maths construction exercise 11.1 || ncert maths class 9 chapter 11 solutions || class 9 math exercise 11.1
3.
(i) Construct the angles of the following measurements:
\( 30^{\circ} \)
\( 30^{\circ} \)
Answer
Draw a ray OA2. Take O as a centre with any radius, draw an arc BC which cuts OA at B.
3. With B and C as centres, draw two arcs which intersect each other at the point E and the perpendicular bisector is drawn.
4. Thus, \( \angle \mathrm{EOA} \) is the required angle making \( 30^{\circ} \) with OA .
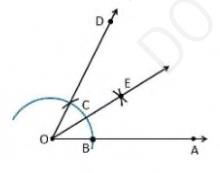
(ii) Construct the angles of the following measurements:
\( 22 \frac{1^{\circ}}{2} \)
\( 22 \frac{1^{\circ}}{2} \)
Answer
\( 22 \frac{1^{\circ}}{2} \)1. Draw an angle \( \angle \mathrm{POA}=90^{\circ} \)
2. Take O as a centre with any radius, draw an arc BC which cuts OA at B and OP at Q
3. Now, draw the bisector from the point B and Q where it intersects at the point \( R \) such that it makes an angle \( \angle R O A=45^{\circ} \).
4. Again, \( \angle \mathrm{ROA} \) is bisected such that \( \angle \mathrm{TOA} \) is formed which makes an angle of \( 22.5^{\circ} \) with OA
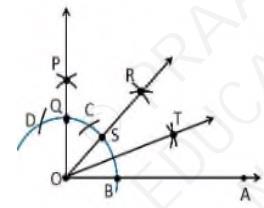
(iii) Construct the angles of the following measurements:
\( 15^{\circ} \)
\( 15^{\circ} \)
Answer
\( 15^{\circ} \)1. An angle \( \angle \mathrm{DOA}=60^{\circ} \) is drawn.
2. Take O as centre with any radius, draw an arc BC which cuts OA at B and OD at C
3. Now, draw the bisector from the point B and C where it intersects at the point E such that it makes an angle \( \angle \mathrm{EOA}=30^{\circ} \).
4. Again, \( \angle \mathrm{EOA} \) is bisected such that \( \angle \mathrm{FOA} \) is formed which makes an angle of \( 15^{\circ} \) with OA.
5. Thus, \( \angle \mathrm{FOA} \) is the required angle making \( 15^{\circ} \) with OA .
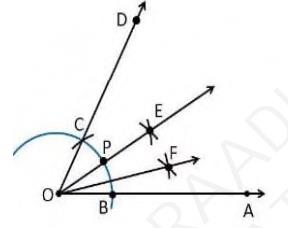
class 9 exercise 11.1 || class 9 maths exercise 11.1 solution || class 9 maths construction exercise 11.1 || exercise 11.1 class 9 || rd sharma class 9 construction || class 9 maths chapter 11 exercise 11.1 || class 9 maths construction exercise 11.1 || ncert maths class 9 chapter 11 solutions || class 9 math exercise 11.1
4.
(i) Construct the following angles and verify by measuring them
by a protractor:
\( 75^{\circ} \)
\( 75^{\circ} \)
Answer
\( 75^{\circ} \)1. A ray OA is drawn.
2. With O as centre draw an arc of any radius and intersect at the point B on the ray OA .
3. With \( B \) as centre draw an \( \operatorname{arc} \mathrm{C} \) and C as centre draw an \( \operatorname{arc} \mathrm{D} \).
4. With D and C as centre draw an arc, that intersect at the point P .
5. Join the points O and P
6. The point that arc intersect the ray OP is taken as Q .
7. With Q and C as centre draw an arc, that intersect at the point R .
8. Join the points O and R
9. Thus, \( \angle \mathrm{AOE} \) is the required angle making \( 75^{\circ} \) with OA .
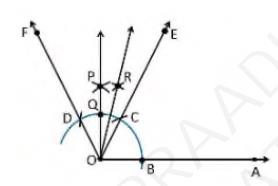
(ii) Construct the following angles and verify by measuring them
by a protractor:
\( 105^{\circ} \)
\( 105^{\circ} \)
Answer
\( 105^{\circ} \)1. A ray OA is drawn.
2. With \( O \) as centre draw an arc of any radius and intersect at the point \( B \) on the ray OA .
3. With \( B \) as centre draw an \( \operatorname{arc} \mathrm{C} \) and C as centre draw an \( \operatorname{arc} \mathrm{D} \).
4. With \( D \) and \( C \) as centre draw an arc, that intersect at the point \( P \).
5. Join the points \( O \) and \( P \)
6. The point that arc intersect the ray OP is taken as Q .
7. With Q and Q as centre draw an arc, that intersect at the point R .
8. Join the points O and R
9. Thus, \( \angle \mathrm{AOR} \) is the required angle making \( 105^{\circ} \) with OA.
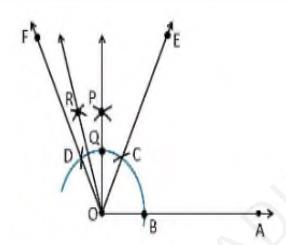
(iii) Construct the following angles and verify by measuring them
by a protractor:
\( 135^{\circ} \)
\( 135^{\circ} \)
Answer
\( 135^{\circ} \)1. Draw a line \(AOA^{\prime}\)
2. Draw an arc of any radius that cuts the line \(AOA^{\prime}\) at the point \( B \) and \(B^{\prime}\)
3. With \( B \) as centre, draw an arc of same radius at the point \( C \).
4. With C as centre, draw an arc of same radius at the point D
5. With D and C as centre, draw an arc that intersect at the point O
6. Join OP
7. The point that arc intersect the ray OP is taken as Q and it forms an angle \( 90^{\circ} \)
8. With \( \mathrm{B}^{\prime} \) and Q as centre, draw an arc that intersects at the point R
9. Thus, \( \angle \mathrm{AOR} \) is the required angle making \( 135^{\circ} \) with OA .
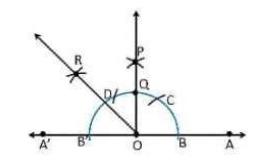
5. Construct an equilateral triangle, given its side and justify
the construction.
Answer
1. Let draw a line segment \( A B=4 \mathrm{~cm} \).2. With \( A \) and \( B \) as centres, draw two arcs on the line segment \( A B \) and note the point as D and E .
3. With D and E as centres, draw the arcs that cuts the previous arc respectively that forms an angle of \( 60^{\circ} \) each.
4. Now, draw the lines from A and B that are extended to meet each other at the point \( C \).
5. Therefore, ABC is the required triangle.
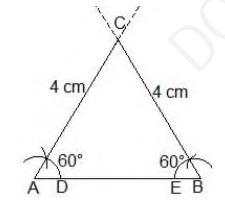
Justification:
From construction, it is observed that
\(
\mathrm{AB}=4 \mathrm{~cm}, \angle \mathrm{A}=60^{\circ} \text { and } \angle \mathrm{B}=60^{\circ}
\)
We know that, the sum of the interior angles of a triangle is equal to \( 180^{\circ} \)
\(
\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ}
\)
Substitute the values
\(\Rightarrow 60^{\circ}+60^{\circ}+\angle \mathrm{C}=180^{\circ}\)
\(\Rightarrow 120^{\circ}+\angle \mathrm{C}=180^{\circ}\)
\(\Rightarrow \angle \mathrm{C}=60^{\circ}\)
While measuring the sides, we get
\( \mathrm{BC}=\mathrm{CA}=4 \mathrm{~cm} \) (Sides opposite to equal angles are equal)
\(\mathrm{AB}=\mathrm{BC}=\mathrm{CA}=4 \mathrm{~cm}\)
\(\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=60^{\circ}\)
Hence, justified.

