NCERT Solutions for Class 10 Maths Chapter 2: Polynomials || CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.4 Math Solution
Discover the complete NCERT Solutions for Class 10 Maths Chapter 2 Polynomials solutions (English Medium), with step-by-step explanations for Exercise 2.3 and Exercise 2.4. This resource ensures a thorough understanding of polynomial concepts, helping Class 10 Maths students excel in their exams. If you have any queries regarding the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials solutions Ex 2.4, drop a comment below, and we’ll assist you at the earliest. NCERT Solutions for Class 10 Maths Chapter 2: Polynomials Class 10 Maths Chapter 2 Polynomials solutions Ex 2.4

NCERT Solutions for Class 10 Maths Chapter 2: Polynomials || CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.4 Math Solution
Exercise-2.4
NCERT Solutions for Class 10 Maths Chapter 2: Polynomials || CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.4 Math Solution
1.
(i) Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
\( 2 x^{3}+x^{2}-5 x+2 ; \frac{1}{2}, 1,-2 \)
\( 2 x^{3}+x^{2}-5 x+2 ; \frac{1}{2}, 1,-2 \)
Answer
\( P(x)=2 x^{3}+x^{2}-5 x+2 \)Now for zeroes, putting the given values in \(x\).
\(\mathrm{P}(\frac{1 }{ 2})=2(\frac{1 }{ 2})^{3}+(\frac{1 }{ 2})^{2}-5(\frac{1 }{ 2})+2\)
\(=(\frac{1 }{ 4})+(\frac{1 }{ 4})-(\frac{5 }{ 2})+2=\frac{(1+1-10+8) }{ 2}=\frac{0 }{ 2}=0\)
\(P(1)=2 \times 1+1-5 \times 1+2=2+1-5+2=0\)
\(P(-2)=2 \times(-2)^{3}+(-2)^{2}-5(-2)+2\)
\(=(2 \times-8)+4+10+2=-16+16\)
\(=0\)
Thus, \( \frac{1 }{ 2},1 \) and \(-2\) are zeroes of given polynomial.
Comparing given polynomial with \( ax^{3}+bx^{2}+cx+\mathrm{d} \) and Taking zeroes as \( \alpha, \beta \), and \( \gamma \), we have
\( \mathrm{a}=2, \mathrm{~b}=1, \mathrm{c}=-5, \mathrm{~d}=2 \) and \( \alpha=\frac{1}{2}, \beta=1, \gamma=-2 \)
Now, We know the relation between zeroes and the coefficient of a standard cubic polynomial as
\(\alpha+\beta+\gamma=-\frac{b}{a}\)
Substituting value, we have
\(\frac{1}{2}+1-2=\frac{1}{2}\)
\(\frac{1}{2}=\frac{1}{2}\)
Since, LHS \( = \) RHS (Relation Verified)
\(\alpha \beta+\beta \gamma+\gamma \alpha=\frac{c}{a}\)
\(\left(\frac{1}{2} \times 1\right)+(1 \times-2)+\left(-2 \times \frac{1}{2}\right)=-\frac{5}{2}\)
\(\frac{1}{2}-2-1=-\frac{5}{2}\)
\(-\frac{5}{2}=-\frac{5}{2}\)
Since LHS \( = \) RHS, Relation verified.
\(\alpha \beta \gamma=-\frac{d}{a}\)
\(\left(\frac{1}{2} \times 1 \times-2\right)=-\frac{2}{2}\)
\(-\frac{2}{2}=-\frac{2}{2}\)
Since LHS \( = \) RHS, Relation verified.
Thus, all three relationships between zeroes and the coefficient is verified.
(ii) Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
\( x^{3}-4 x^{2}+5 x-2 ; 2,1,1 \)
\( x^{3}-4 x^{2}+5 x-2 ; 2,1,1 \)
Answer
\( p(x)=x^{3}-4 x^{2}+5 x-2 \)Now for zeroes, put the given value in \( x \).
\(P(2)=2^{3}-4(2)^{2}+5 \times 2-2=8-16+10-2=18-18=0\)
\(P(1)=1^{3}-4(1)^{2}+5 \times 1-2=1-4+5-2=6-6=0\)
\(P(1)=1^{3}-4(1)^{2}+5 \times 1-2=1-4+5-2=6-6=0\)
Thus, 2, 1, 1 are the zeroes of the given polynomial.
Now,
Comparing the given polynomial with \( a x^{3}+b x^{2}+c x+d \), we get \( \mathrm{a}=1, \mathrm{~b}=-4 . \mathrm{c}=5, \mathrm{~d}=-2 \) and \( \alpha=2, \beta=1, \gamma=1 \)
Now,
\(
2+1+1=\frac{4}{1}\)
\(4=4\)
\(\alpha \beta+\beta \gamma+\gamma \alpha=\frac{c}{a}\)
\((2 \times 1)+(1 \times 1)+(1 \times 2)=\frac{5}{1}\)
\(2+1+2=5\)
\(5=5\)
\(\alpha \beta \gamma=-\frac{d}{a}\)
\(2 \times 1 \times 1=2\)
\( 2=2 \)
Thus, all three relationships between zeroes and the coefficient is verified.
2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as \( 2,-7,-14 \) respectively.
Answer
For a cubic polynomial equation, \( ax^{3}+bx^{2}+cx+\mathrm{d} \), and zeroes \( \alpha, \beta \) and \( \gamma \)we know that
\(\alpha+\beta+\gamma=\frac{-b}{a}\)
\(\alpha \beta+\beta \gamma+\gamma \alpha=\frac{c}{a}\)
\(\alpha \beta\gamma=\frac{-d}{a}\)
Let the polynomial be \( ax^{3}+bx+cx+\mathrm{d} \), and zeroes \( \alpha, \beta \) and \( \gamma \).
A cubic polynomial with respect to its zeroes is given by, \( x^{3}- \) (sum of zeroes) \( x^{2}+ \) (Sum of the product of roots taken two at a time) \( x- \) Product of Roots \( =0 \)
\(x^{3}-(2) x^{2}+(-7) x-(-14)=0\)
\(x^{3}-(2) x^{2}+(-7) x+14=0\)
Hence, the polynomial is \( x^{3}-2 x^{2}-7x+14 \).
NCERT Solutions for Class 10 Maths Chapter 2: Polynomials || CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.4 Math Solution
3. If the zeroes of the polynomial \( x^{3}-3 x^{2}+x+1 \) are \( (a-b) \), \( a \) and \( (a \) \( +b) \). Find \( a \) and \( b \).
Answer
Given\(P(x)=x^{3}-3 x^{2}+x+1\)
Zeroes are \( =\mathrm{a}-\mathrm{b}, \mathrm{a}+\mathrm{b}, \mathrm{a} \)
Comparing the given polynomial with \( mx^{3}+nx^{2}+px+\mathrm{q} \), we get,
\(=\mathrm{m}=1, \mathrm{n}=-3, \mathrm{p}=1, \mathrm{q}=1\)
Sum of zeroes \( =\mathrm{a}-\mathrm{b}+\mathrm{a}+\mathrm{a}+\mathrm{b}=-\frac{n}{m} \)
\(3 a=-\frac{-3}{1}=3\)
\(a=\frac{3}{3}=3\)
The zeroes are \( =(1-b), 1 \) and \( (1+b) \)
Product of zeroes \( =(1-b)(1+b) \)
\((1-b)(1+b)=\frac{-q }{ m}\)
\(1-b^{2}=-\frac{1}{1}=-1\)
\(b^{2}=2\)
\(b= \pm \sqrt{2}\)
So,
We get, \( \mathrm{a}=1 \) and \( \mathrm{b}= \pm \sqrt{2} \)
4. If two zeroes of the polynomial \( x^{4}-6 x^{3}-26 x^{2}+138 x-35 \) are \( 2 \pm \) \( \sqrt{3} \) find other zeroes.
Answer
Given:\( 2+\sqrt{3} \) and \( 2-\sqrt{3} \) are zeroes of given equation,
Therefore, \( (x-2+\sqrt{3})(x-2-\sqrt{3}) \) should be a factor of given equation.
Also, \( (x-2+\sqrt{3})(x-2-\sqrt{3 } )\)
\(=x^{2}-2 x-\sqrt{3 } x-2 x+4+2 \sqrt{ 3} +\sqrt{3} x-2 \sqrt{3} \) \( -3 \)
\(=x^{2}-4 x+1\)
To find other zeroes, we divide given equation by \( x^{2}-4 x+1 \)

We get ,
\(x^{4}-6 x^{3}-26 x^{2}+138 x-35=\left(x^{2}-4 x+1\right)\left(x^{2}-2 x-35\right)\)
Now factorizing \( x^{2}-2 x-35 \) we get,
\( x^{2}-2 x-35 \) is also a factor of given polynomial and \( x^{2}-2 x-35=(x- 7)\) \( (x+5) \)
The value of polynomial is also zero when, \( x-7=0 \)
or \( x=7 \)
And, \( x+5=0 \)
Or \( x=-5 \)
Hence, 7 and \(-5\) are also zeroes of this polynomial.
5. If the polynomial \( x^{4}-6 x^{3}+16 x^{2}-25 x+10 \) is divided by another polynomial \( x^{2}-2 k+k \) the remainder comes out to be \( x+a \), find \( k \) and a.
Answer
To solve this question divide \( x^{4}-6 x^{3}+16 x^{2}-25 x+10 \) by \( x^{2}-2 x+ \) k by long division methodLet us divide, by \( x^{4}-6 x^{3}+16 x^{2}-25 x+10 \) by \( x^{2}-2 x+k \)
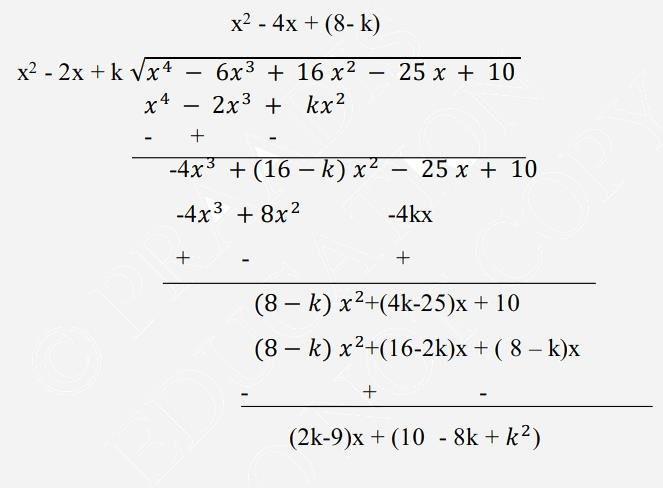
So, remainder \( =(2 k-9) x+\left(10-8 \mathrm{k}+\mathrm{k}^{2}\right) \)
But given remainder \( =x+a \)
\(\Rightarrow(2 k-9) x+\left(10-8 k+k^{2}\right)=x+a \)
Comparing coefficient of \(x\), we have \( 2 \mathrm{k}-9=1\)
\( \Rightarrow 2 \mathrm{k}=10 \)
\(\Rightarrow \mathrm{k}= 5\) and Comparing constant term, \( 10-8 \mathrm{k}+\mathrm{k}^{2}=\mathrm{a} \)
\(\Rightarrow \mathrm{a}=10-8(5)+5^{2}\)
\( \Rightarrow \mathrm{a}=10-40+25 \)
\(\Rightarrow \mathrm{a}=-5 \). So, the value of k is 5 and a is \(-5\) .
NCERT Solutions for Class 10 Maths Chapter 2: Polynomials || CBSE Class 10 Maths Chapter 2 Polynomials solutions Ex 2.4 Math Solution
Central Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.3

