NCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.1 Math Solution
Get the complete NCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables, covering Exercise 3.1. This free resource helps you understand key concepts and solve problems with ease, perfect for CBSE Class 10 students preparing for exams using NCERT Maths materials. We hope the NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.1 help you. If you have any queries regarding NCERT Maths Solutions Chapter 3 Pair of Linear Equations in Two Variables Exercise 3.1, drop a comment below, and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.1 Math Solution
Exercise-3.1
NCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.1 Math Solution
To Represent the situations algebraically and graphically we need to find the linear equations for these situations. Let present age of Aftab \( =\mathrm{x} \)
Let present age of his daughter \( =\mathrm{y} \)
Then, seven years ago the age of Aftab and his daughter must have been seven less than their present ages, Age of Aftab seven years ago \( =\mathrm{x}- \) 7
Age of Daughter seven years ago \( =\mathrm{y}-7 \)
According to the question,
Seven years ago, Aftab was seven times as old as his daughter, So
\(x-7=7(y-7)\)
\(\Rightarrow x-7=7 y-49\)
\(\Rightarrow x=7 y-42\)
Now for finding different points of this equation, we can either take different values of x and put them in the equation to obtain values of y or vice versa
Putting \( y=5,6 \) and \(7\) in equation \( (i) \), we get,
\(\text { For } y=5\)
\(x=7 \times 5-42\)
\(=35-42=-7 \text { For } x=6\)
\(x=7 \times 6-42\)
\(=42-42=0 \text { For } y=7\)
\(x=7 \times 7-42\)
\(=49-42=7\)
\(\begin{array}{|l|l|l|l|}
\hline x & -7 & 0 & 7 \\
\hline y & 5 & 6 & 7 \\
\hline
\end{array}\)
Thus we got 3 points to plot on graph for this equation.
Three years from now,
Age of Aftab \( =x+3 \)
Age of Daughter \( =y+3 \)
According to the question,
\(\Rightarrow x+3=3(y+3) \Rightarrow x+3=3 y+9 \Rightarrow x=3 y+6\)
Now for finding different points of this equation, we can either take different values of \( x \) and put them in equation to obtain values of \( y \) or vice versa
Putting \( \mathrm{x}=0,3 \) and \(6\)
\(\begin{array}{|l|l|l|l|}
\hline x & 0 & 3 & 6 \\
\hline y & -2 & -1 & 0 \\
\hline
\end{array}\)
Thus we got 3 points to plot on graph for this equation.
Algebraic representation
\(x-7 y=-42\) (i)
\(x-3 y=6\) (ii)
Graphical representation:
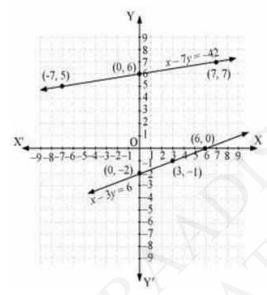
NCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.1 Math Solution
Download the Math Ninja App Now Ninja AppLet cost of one bat \( = \) Rs. x
Let cost of one ball = Rs. y
In first case, three bats and 6 balls cost him 3900 rupees. Therefore our equation becomes
\(\Rightarrow 3 x+6 y=3900\)...(i)
Dividing equation by 3 both side
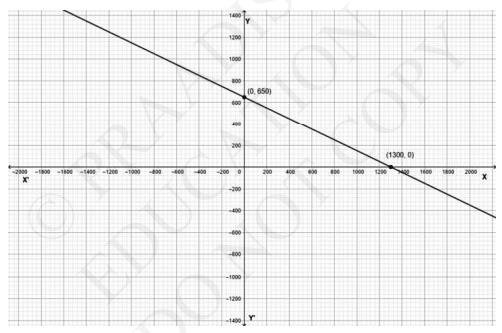
\(\Rightarrow x+2 y=1300\)
\(\Rightarrow x=1300-2 y\)
For plotting the equation of graph, take different values of \( y \) and obtain the value of \( x \) from equation or you can do vice versa. At \( y=0 \Rightarrow x= \) \( 1300-2(0) \Rightarrow \mathrm{x}=1300 \) Now finding the value at \( \mathrm{x}=0 \Rightarrow 0=1300 \) \( 2 \mathrm{y} \Rightarrow 2 \mathrm{y}=1300 \Rightarrow \mathrm{y}=650 \)
\(\begin{array}{|l|l|l|}
\hline X & 0 & 1300 \\\hline Y & 650 & 0 \\\hline
\end{array}\)
From above points, we make the graph as follows [Graphic representation]
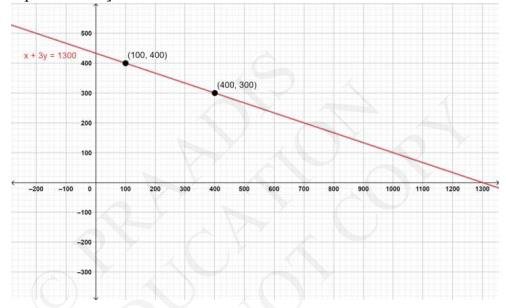
In second case he buys one bat and 3 balls for 1300 , therefore,
\(\Rightarrow x+3 y=1300\)...(ii) \(\quad \) [Algebraic representation]
\( \Rightarrow x=1300-3 y\)
\(\text { At } y=400 \)
\(\Rightarrow \mathrm{x}=1300-3(400) \)
\(\Rightarrow \mathrm{x}=100 \text { At } \mathrm{y}=300 \)
\(\Rightarrow \mathrm{x}=1300-3(300) \)
\(\Rightarrow \mathrm{x}=400\)
\(\begin{array}{|l|l|l|}
\hline x & 100 & 400 \\
\hline y & 400 & 300 \\
\hline
\end{array}\)
From above points, we make the graph as follows, [Graphical representation]
 s
sNCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.1 Math Solution
Download the Math Ninja App Now Ninja AppLet the cost of each kg of grapes \( = \) Rs. Y
According to the question,
Cost of 2 kg of Apples \( =2 \mathrm{x} \)
Cost of 1 kg of grapes \( =\mathrm{y} \)
\(2 x+y=160\ldots(i)\)
\(2 x=160-y\)
\(x=\frac{16-y}{2}\)
Putting \( y=20,40 \) and 60 we get,
\(x=\frac{(160-20)}{2}=70\)
\(x=\frac{(160-40))}{2}=60\)
\(x=\frac{(160-60)}{2}=50\)
\(\begin{array}{|l|l|l|l|}\hline X & 50 & 60 & 70 \\\hline Y & 60 & 40 & 20 \\\hline\end{array}\)
Algebraic Representation: \( 2 \mathrm{x}+\mathrm{y}=160 \)
Graphical Representation:
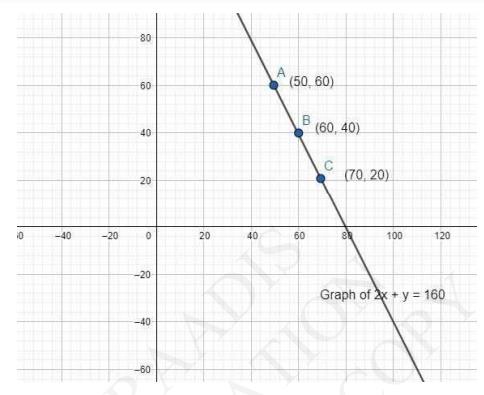
Now taking another case
Cost of 4 kg of apples and 2 kg of grapes is Rs.300.................................(Given)
So, \( 4 \mathrm{x}+2 \mathrm{y}=300 \ldots(ii)\)
Dividing the equation by 2 , we get,
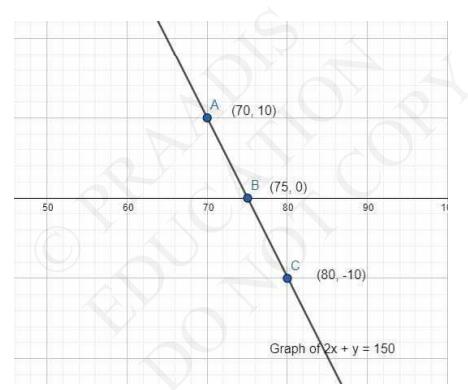
\(2 x+y=150\)
\(y=150-2 x\)
Putting \( \mathrm{x}=70,75 \) and 80 we get,
\(y=150-2 \times 70=10\)
\(y=150-2(75)=0\)
\(y=150-2(80)=150-160=-10\)
\(\begin{array}{|l|l|l|l|}
\hline X & 70 & 75 & 80 \\\hline Y & 10 & 0 & -10 \\
\hline\end{array}\)
Algebraic representation:
\(4 x+2 y=300\)
Graphical representation:
NCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.1 Math Solution
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.3

