NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Explore the NCERT Solutions for Class 10 Maths Chapter 5: Arithmetic Progressions (English Medium), with detailed explanations for Exercise 5.3. This resource is designed to simplify complex Arithmetic Progressions, helping Class 10 Maths students grasp the subject effortlessly. For any queries regarding NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3, feel free to leave a comment, and we’ll respond as soon as possible. Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3. NCERT Solutions for Class 10 Maths Chapter 5: Arithmetic Progressions (English Medium)

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Exercise 5.3

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Download the Math Ninja App Now

1. Find the sum of the following APs:

(i)

$2,7,12, \ldots$ , to 10 terms.

Answer

Here,

$\mathrm{a}=2, \mathrm{~d}=5$ and

$\mathrm{n}=10$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{10}=\frac{10}{2}[2 \times 2+(10-1) 5]$

$=5(4+45)$

$=5 \times 49$

$=245$
thus, sum of the 10 terms of given

$\operatorname{AP}\left(\mathrm{S}_{\mathrm{n}}\right)=245$

(ii)

$-37,-33,-29, \ldots$ , to 12 terms.

Answer

Here,

$a=-37, d=4$ and

$n=12$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{12}=\frac{12}{2}[2 \times(-37)+(11) 4]$

$=6(-74+44)$

$=6 \times(-30)$

$=-180$
Thus, sum of the 12 terms of given

$A P\left(\mathrm{S}_{\mathrm{n}}\right)=-180$

(iii)

$0.6,1.7,2.8, \ldots$ , to 100 terms.

Answer

Here,

$\mathrm{a}=0.6, \mathrm{~d}=1.1$ and

$\mathrm{n}=100$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{100}=\frac{100}{2}[2 \times(0.6)+(99) .1]$

$50(1.2+108.9)$

$=50 \times(110.1)$

$=5505$
Thus, sum of the 100 terms of given AP

$(\mathrm{S} 100)=5505$

(iv)

$\frac{1}{15}, \frac{1}{12}, \frac{1}{10}, \ldots$ , to 11 terms

Answer

Here,

$a=\frac{1}{15}, n=11$

$d=\frac{1}{12}-\frac{1}{5}=\frac{1}{60}$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{11}=\frac{11}{2}\left[2 \times\left(\frac{1}{15}\right)+(10) \frac{1}{60}\right]$

$=\frac{11}{2}\left(\frac{2}{15}+\frac{1}{6}\right)$

$=\frac{11}{2} \times\left(\frac{4+5}{30}\right)$

$=\frac{33}{20}$
Thus, sum of the 100 terms of given AP

$\left(\mathrm{S}_{\mathrm{n}}\right)=\frac{33}{20}$

2. Find the sums given below:

(i)

$7+10 \frac{1}{2}+14+\cdots+84$

Answer

Here,

$\mathrm{a}=7, \mathrm{~d}=3.5$ and last term

$=84$
Number of terms can be calculated as follows;

$\mathrm{an}=a+(\mathrm{n}-1) \mathrm{d}$
Or,

$84=7+(\mathrm{n}-1) 3.5$
Or,

$(\mathrm{n}-1) 3.5=84-7$
Or,

$\mathrm{n}-1=\frac{77 }{ 3.5}=22$
Or,

$\mathrm{n}=23$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{23}=\frac{23}{2}[2 \times(7)+(22) .5]$

$=\frac{23}{2}(14+77)$

$=\frac{23}{2} \times(91)$

$=1046 \frac{1}{2}$

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Download the Math Ninja App Now

(ii)

$34+32+30+\ldots+10$

Answer

Here,

$\mathrm{a}=34, \mathrm{d}=-2$ and last term

$=10$
Number of terms can be calculated as follows:

$\mathrm{an}=\mathrm{a}+(\mathrm{n}-1) \mathrm{d}$
Or,

$10=34+(n-1)(-2)$
Or,

$10=34-(\mathrm{n}-1)(2)$
Or,

$(\mathrm{n}-1) 2=34-10=24$
Or,

$\mathrm{n}-1=12$
Or,

$\mathrm{n}=13$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{13}=\frac{13}{2}[2 \times(34)+(12)(-2)]$

$=\frac{13}{2}[68+(-24)]$

$=\frac{13}{2} \times(44)$

$=286$
Thus, sum of the given

$\mathrm{AP}(\mathrm{Sn})= 286$

(iii)

$-5+(-8)+(-11)+\ldots+(-230)$

Answer

Here,

$a=-5, d=-3$ and last term

$=-230$
Number of terms can be calculated as follows:

$\text {an }=a+(n-1) d$

$\text {Or, }-230=-5+(n-1)(-3)$

$\text {Or, }-230=-5-(n-1) 3$
Or,

$(\mathrm{n}-1) 3=-5+230=225$
Or,

$\mathrm{n}-1=75$
Or,

$\mathrm{n}=76$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{23}=\frac{76}{2}[2 \times(-5)+(-3) 75]$

$=\frac{76}{2}(-10-225)$

$38 \times(-235)$

$=-8930 .$

3. In an AP :

(i) given

$a=5, d=3, a_{n}=50$ , find

$n$ and

$s_{n}$ .

Answer

To find:

$\mathrm{n}, \mathrm{S}_{\mathrm{n}}$
Given:

$a_{n}=50$

$a=5 d=3$
We know, nth term of an AP is given by

$a_{n}=a+(n-1) d$
where

$a$ and

$d$ are first term and common difference respectively and

$n$ are the number of terms of the A.P
Number of terms can be calculated as follows:

$a_{n}=a+(n-1) d$
Or,

$50=5+(\mathrm{n}-1) 3$
Or,

$(n-1) 3=50-5=45$
Or,

$\mathrm{n}-1=15$
Or,

$\mathrm{n}=16$
Sum of N terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$\mathrm{S}_{16}=\frac{16}{2}[2\times(5)+(1 5) 3]$

$=8(10+45)$

$=8 \times 55$

$=440$

$\mathrm{S}_{\mathrm{n}}=440$

(ii) given

$a=7, a_{13}=35$ , find

$d$ and

$S_{13}$ .

Answer

To find: d and

$\mathrm{S}_{13}$
Given:

$\mathrm{a}=7$

$a_{13}=35$
We know, nth term of an AP is

$a_{n}=a+(n-1) d$
where a and d are first term and common difference respectively.
So, Common difference can be calculated as follows:

$a_{n}=a+(n-1) d$
Or,

$35=7+12 d$
Or,

$12 \mathrm{d}=35-7=28$
Or,

$\mathrm{d}=\frac{7 }{ 3}$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{16}=\frac{13}{2}\left[2 \times(7)+(12) \frac{7}{3}\right]$

$=\frac{13}{2}(14+28)$

$=\frac{13}{2} \times(42)$

$=273$

$S_{13}=273$

(iii) given

$d=3, a_{12}=37$ find

$a$ and

$S_{12}$

Answer

(iii) To Find: a,

$\mathrm{S}_{12}$
Given:

$\mathrm{d}=3$

$\mathrm{a}_{12}=37$
We know, nth term of an AP is

$a n=a+(n-1) d$
where a and d are first term and common difference respectively.
Therefore, First term can be calculated as follows:

$\mathrm{a}_{\mathrm{n}}=\mathrm{a}+(\mathrm{n}-1) \mathrm{d}$
Or,

$37=\mathrm{a}+11 \times 3$
Or,

$\mathrm{a}=37-33=4$

$a=4$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{12}=\frac{13}{2}[2 \times(4)+(11) 3]$

$=6(8+33)$

$=6 \times 41$

$\mathrm{~S}_{12}=246$

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Download the Math Ninja App Now

(iv) given

$\mathrm{a}_{3}=15, \mathrm{~S}_{10}=125$ find

$d$ and

$\mathrm{a}_{10}$ .

Answer

To find: d,

$a_{10}$
Given:

$a_{3}=15$

$\mathrm{S}_{10}=125$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$S_{10}=\frac{10}{2}[2 \times(a)+(9) d]$

$125=5(2 \mathrm{a}+9 \mathrm{d})$

$25=2 \mathrm{a}+9 \mathrm{d}\quad \ldots\ldots\text{(i)}$
We know, nth term of an AP is

$a_{n}=a+(n-1) d$
where a and d are first term and common difference respectively.
According to the question; the 3rd term is 15, which means;

$a+2 d=15 \quad \ldots\ldots\text{(ii)}$
Now,
Subtracting equation 2 times eq(ii) from equation eq(i), we get;

$(2 a+9 d)-2(a+2 d)=25-30$
Or,

$2 a+9 d-2 a-4 d=-5$
Or,

$5 \mathrm{d}=-5 \mathrm{d}=-1$
Now,
Substituting the value of

$d$ in equation (2), we get;

$a+2(-1)=15$
Or,

$a-2=15$
Or,

$\mathrm{a}=17$

$10^{\text {th}}$ term can be calculated as follows;

$\mathrm{a}_{10}=\mathrm{a}+9 \mathrm{d}$

$=17-9=8$

$a_{10}=8$

(v) given

$d=5, S_{9}=75$ , find

$a$ and

$a_{9}$ .

Answer

To find: a and

$a_{9}$
Given:

$d=5$

$S_{9}=75$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$75=\frac{9}{2}[2 \times(a)+(8) 5]$

$75=\frac{9}{2}(2 a+40)$

$\frac{50}{3}=2 a \times 40$

$a=-\frac{35}{3}$
Now,
We know, nth term of an AP is

$a_{n}=a+(n-1) d$
where a and d are first term and common difference respectively.

$9^{\text {th}}$ term can be calculated as follows:

$a_{9}=a+8 d$

$=-\frac{35}{3}+40$

$=\frac{85}{3}$

(vi) given

$\mathrm{a}=2, \mathrm{~d}=8, \mathrm{~S}_{\mathrm{n}}=90$ , find n and

$\mathrm{a}_{\mathrm{n}}$ .

Answer

To find

$: \mathrm{n}$ and an
Given:

$\mathrm{a}=2$

$\mathrm{d}=8$

$\mathrm{Sn}=90$
Sum of n terms can be given as follows

$S=\frac{N}{2}[2 a+(n-1) d]$

$90=\frac{N}{2}[2 \times(2)+(N-1) 8]$

$90=\frac{N}{2}(4+8 N-8)$

$90=N(2+4 N-4)$

$4 N^{2}-2 N-90=0$

$2 N^{2}-N-45=0$
For solving this quadratic equation, we have to factor 1 in such a way that product comes out to be 90 and the difference should be 1

$(2 \mathrm{N}+9)(\mathrm{N}-5)$
Hence,

$n=-\frac{9 }{ 2}$ and

$n=5$
Rejecting the negative value,
We have

$\mathrm{n}=5$
We know, nth term of an AP is

$a_{n}=a+(n-1) d$
where a and

$d$ are first term and common difference respectively.
Now,

$5^{\text {th}}$ term will be:

$a_{5}=a+(5-1) d$

$a_{5}=a+4 d$

$=2+4 \times 8$

$=2+32=34$

$\mathrm{a}_{5}=34$

(vii) given

$a=8, a_{n}=62, S_{n}=210$ find

$n$ and

$d$ .

Answer

To find: n and d
Given:

$a=8$

$a_{n}=62$

$S_{n}=210$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$210=\frac{N}{2}[a+a+(n-1) 8]$
Since,

$a_{n}=a+(n-1) d$ , we have

$420=n(8+62)$

$420=\mathrm{n} \times 70$

$\mathrm{n}=6$
Now, for calculating d:
we know that

$a_{n}=a+(n-1) d$

$a_{6}=a+5 d$
Or,

$62=8+5 \mathrm{d}$
Or,

$5 \mathrm{d}=62-8=54$
Or,

$\mathrm{d}=\frac{54 }{ 5}$
Common difference,

$d=\frac{54 }{ 5}$

(viii) given

$\mathrm{a}_{\mathrm{n}}=4, \mathrm{~d}=2, \mathrm{~S}_{\mathrm{n}}=-14$ find n and a .

Answer

To find: n and a
Given:

$a_{n}=4$

$d=2 S_{n}=-14$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$-14=\frac{n}{2}[a+a+(n-1) d]$

$-28=n(a+4)$

$n=\frac{-28}{a+4} \quad \ldots\ldots\text{(i)}$
We know;
We know, nth term of an AP is

$a_{n}=a+(n-1) d$
where a and d are the first term and common difference respectively.
therefore,

$4=a+(n-1) 2$
Or,

$4=\mathrm{a}+2 \mathrm{n}-2$
Or,

$a+2 n=6$
Or,

$2 \mathrm{n}=6-\mathrm{a}$
Or,

$\mathrm{n}=\frac{(6-\mathrm{a}) }{ 2}\quad \ldots\ldots\text{(ii)}$
Using (i) and (ii):

$\frac{-28}{a+4}=\frac{6-a}{2}$
Cross multiplying, we get

$-56=(6-a)(a+4)$

$24+2 a-a^{2}=-56$

$a^{2}-2 a-80=0$
Factorizing 2 in such a way that product of the two terms is 80 and their difference is 2

$(a+8)(a-10)=0$
Therefore,

$\mathrm{a}=-8$ and

$\mathrm{a}=10$
As a is smaller than 10 and d has positive value, hence we'll take

$\mathrm{a}=- 8$
Now, we can find the number of terms as follows:

$\mathrm{a}_{\mathrm{n}}=\mathrm{a}+(\mathrm{n}-1) \mathrm{d}$

$4=-8+(\mathrm{n}-1) 2$

$(\mathrm{n}-1) 2=4+8=12$

$\mathrm{n}-1=6, \mathrm{n}=7$
Hence,

$\mathrm{n}=7$ and

$\mathrm{a}=-8$

(ix) given

$\mathrm{a}=3, \mathrm{n}=8, \mathrm{~S}=192$ , find d

Answer

To find: d
Given:

$\mathrm{a}=3$

$\mathrm{n}=8 \mathrm{S}_{\mathrm{n}}=192$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$192=\frac{8}{2}[2 \times 3+7 d]$

$192=4(6+7 \mathrm{d})$

$7 \mathrm{d}=42$

$\mathrm{d}=6$

(x) given

$1=28, S=144$ , and there are total 9 terms. Find a.

Answer

To Find: a
Given:

$1=28, \mathrm{S}=144$
Sum of n terms can be given as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$144=\frac{9}{2}\left[a+a_{n}\right]$

$288=\mathrm{n}(\mathrm{a}+28)$

$9 \mathrm{a}+252=288$

$9 \mathrm{a}=288-252$

$9 \mathrm{a}=36$

$\mathrm{a}=4$

4. How many terms of the AP :

$9,17,25, \ldots$ must be taken to give a sum of 636 ?

Answer

Given that,

$\mathrm{a}=9, \mathrm{d}=8$ and

$\mathrm{S}_{\mathrm{n}}=636$
Let no of terms be N.
Now
We know:

$S=\frac{N}{2}[2 a+(n-1) d]$

$636=\frac{N}{2}[2 \times(9)+(N-1) 8]$

$\Rightarrow 636=\frac{N}{2}(18+8 N-8)$

$\Rightarrow 636=\mathrm{N}(9+4 \mathrm{N}-4)$

$\Rightarrow 636=9 \mathrm{N}+4 \mathrm{N}^{2}-4 \mathrm{N}$

$\Rightarrow 4 \mathrm{N}^{2}+5 \mathrm{N}-636=0$
Now to factorize the above quadratic equation, we need to make the product

$( 636.4=2544 )$ and difference should be

$5$

$\Rightarrow 4 \mathrm{N}^{2}+53 \mathrm{N}- 48 \mathrm{N}-636=0$

$\Rightarrow \mathrm{N}(4 \mathrm{N}+53)-12(4 \mathrm{N}+53)=0$

$\Rightarrow(\mathrm{N}-12)(4 \mathrm{N}+53)=0$
Now,

$\mathrm{N}=-\frac{53 }{ 4}$ and

$\mathrm{N}=12$
Taking the integral value and rejecting the fractional value, we have

$\mathrm{n}=12$ .

5. The first term of an

$A P$ is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.

Answer

Sum of n terms of an AP is given by,

$S_{n}=\frac{n}{2}\left(a+a_{n}\right)$
where 'a' is first term of

$\mathrm{AP}, \mathrm{n}$ is the number of terms of AP and 'an' is last term of AP.
Given, First term, a

$=5$ and last term, an

$=45$
Also, sum

$=400$ Putting the values in the formula, we get

$400=\frac{n}{2}$

$( 5+ 45)$

$\Rightarrow 800=50 \mathrm{n} n=\frac{800}{50}$

$\Rightarrow \mathrm{n}=16$ .
i.e. there are 16 terms in given AP.
Now the nth term of an

$A P$ is given by the formula,

$a_{n}=a+(n-1) d$
where,

$a$ is the first term,

$n$ is the number of terms,

$a_{n}$ is the

$n$ th term and

$d$ is the common difference.

$45=5+(16-1) \times d \Rightarrow 15 d=40$

$\Rightarrow d=\frac{40 }{ 15}$
Therefore, common difference of AP is

$\frac{8 }{ 3}$ .

6. The first and the last terms of an AP are 17 and 350 respectively. If the common differenceis 9 , how many terms are there and what is their sum?

Answer

We have;
First term,

$\mathrm{a}=17$ , Last term,

$\mathrm{an}=350$ and
Common difference,

$d=9$
We know, nth term formula:

$\mathrm{a}_{\mathrm{n}}=\mathrm{a}+(\mathrm{n}-1) \mathrm{d}$

$350=17+(\mathrm{n}-1) 9$

$(\mathrm{n}-1) 9=350-17$

$\mathrm{n}-1=\frac{333 }{ 9}=37$

$\mathrm{n}=38$
and we know, sum of '

$n$ ' terms of an AP if first and last term is given is

$S_{n}=\frac{n}{2}\left(a+a_{n}\right)$

$=\frac{38}{2}[17+350]$

$=19 \times 367$

$=6973$

7. Find the sum of first 22 terms of an

$A P$ in which and 22nd term is 149.

Answer

We have;

$\mathrm{n}=22, \mathrm{d}=7$ and

$\mathrm{a}_{22}=149$
where n is number of terms and
d is common difference.
We know;

$a_{n}=a+(n-1) d$

$\Rightarrow 149=\mathrm{a}+(22-1) 7$

$\Rightarrow 149=\mathrm{a}+147$

$\Rightarrow \mathrm{a}=149-147$

$\Rightarrow \mathrm{a}=2$
The sum can be calculated as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$=\frac{22}{2}[2+149]$

$=11 \times 151$

$=1661$

8. Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively.

Answer

To Find:

$\mathrm{S}_{51}$
Given:

$\mathrm{a}_{2}=14, \mathrm{a}_{3}=18$ and

$n=51$
We have;

$\mathrm{a}_{2}=14, \mathrm{a}_{3}=18$ and

$\mathrm{n}=51$
We know,

$d=a_{3}-a_{2}=18-14=4$
Therefore,

$\mathrm{d}=4$

$a_{2}-a=4$

$14-a=4$

$a=10$
So, first term

$=10$
Now, sum can be calculated as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$
Where, a and d are first term and common difference respectively.

$=\frac{51}{2}[2 \times 10+50 \times 4]$

$=51 \times\frac{(20+200) }{ 2}$

$=51 \times 110$

$=5610$

$S_{51}=5610$

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Download the Math Ninja App Now

$Mathninja.in$

9. If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.

Answer

Given:

$S_{7}=49, S_{17}=289$
Sum of

$n$ terms of an A.P is given by the formula,

$S_{n}=\frac{n}{2}[2 a+(n-1) d]$
where,

$\mathrm{S}=$ Sum,

$\mathrm{n}=$ number of terms,

$\mathrm{a}=$ first term and

$\mathrm{d}=$ common difference.

$S_{7}=49$
Therefore,

$49=\frac{7}{2}(2 a+(7-1) d)$

$\Rightarrow 49=7(\mathrm{a}+3 \mathrm{d})$

$\Rightarrow 7=\mathrm{a}+3 \mathrm{d}$

$\Rightarrow \mathrm{a}+3 \mathrm{d}=7\quad \ldots\ldots\text{[i]}$
Similarly,

$S_{17}=\frac{17}{2}[a+(17-1) d]$

$289=17(\mathrm{a}+8 \mathrm{d})$

$17=\mathrm{a}+8 \mathrm{d}$

$\mathrm{a}+8 \mathrm{d}=17\quad \ldots\ldots\text{[ii]}$
Subtracting [1] from [2] we get;

$a+8 d-a-3 d=17-7$

$\Rightarrow 5 d=10$

$\Rightarrow d=2$
Using the value of

$d$ in the equation [1], we can find 'a' as follows:

$a+3 d=7$

$\Rightarrow a+6=7$

$\Rightarrow a=1$
Using the values of a and d; we can find the sum of first n terms as follows:

$S_{n}=\frac{n}{2}[2(1)+(n-1) 2]$

$S_{n}=\frac{n}{2}[2+2 n-2]$

$\Rightarrow S=n^{2}$

10.

(i) Show that

$a_{1}, a_{2}, \ldots \ldots, a_{n}$ form an AP where

$a_{n}$ is defined as below

$a_{n}=3+4 n$
Also find the sum of the first 15 terms.

Answer

Let us take different values for a, i.e.

$1,2,3$ and so on

$\mathrm{a}=3+4=7$

$\mathrm{a}_{2}=3+4 \times 2=11$

$\mathrm{a}_{3}=3+4 \times 3=15$

$\mathrm{a}_{4}=3+4 \times 4=19$
Here; each subsequent member of the series is increasing by 4 and hence it is an AP.
The sum of "n" terms is given as:

$\text {Sum}=\frac{n}{2}[2 a+(n-1) d]$
where,

$\mathrm{n}=$ no. of terms

$\mathrm{a}=$ first term

$\mathrm{d}=$ common difference

$\therefore$ The sum of first 15 terms is given as:

$=(\frac{15 }{ 2})[2 \times 7+(15-1) \times 4]$

$=(\frac{15 }{ 2})[14+(14) \times 4]$

$=(\frac{15 }{ 2})[70]$

$=525$

(ii) Show that

$a_{1}, a_{2}, \ldots \ldots, a_{n}$ form an AP where

$a_{n}$ is defined as below

$a_{n}=9-5 n$
Also find the sum of the first 15 terms.

Answer

Let us take values for a, i.e.

$1,2,3$ and so on

$\mathrm{a}=9-5=4$

$\mathrm{a}_{2}=9-5 \times 2=-1$

$\mathrm{a}_{3}=9-5 \times 3=-6$

$\mathrm{a}_{4}=9-5 \times 4=-11$
Here; each subsequent member of the series is decreasing by 5 and hence it is an AP.

$\therefore$ The sum of first 15 terms is given as:

$=(\frac{15 }{ 2})[2 \times 4+(15-1) \times-5]$

$=(\frac{15 }{ 2})[8+(14) \times-5]$

$=(\frac{15 }{ 2})[8-70]$

$=15(-31)$

$=-465$

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Download the Math Ninja App Now

11. If the sum of the first

$n$ terms of an

$A P$ is

$4 n-n^{2}$ , what is the first term (that is

$\mathrm{S}_{1}$ ) ?
What is the sum of first two terms? What is the second term? Similarly, find the 3rd, the 10th and the nth terms.

Answer

As the sum till first term will only contain first term,

$\mathrm{S}_{1}=\mathrm{a}_{1}$
We can find the first term as follows:

$\mathrm{S}_{\mathrm{n}}=4 \mathrm{n}-\mathrm{n}^{2}$
So, by putting the values in place of 1 we will get the sum till that term

$\mathrm{S}_{1}=4 \times 1-1^{2}=3$
Now; sum of first two terms can be calculated as follows:

$\mathrm{S}_{2}=4 \times 2-2^{2}$

$=8-4=4$
Hence,

$\mathrm{S}_{2}=4$
Now we know by the formula that:

$S_{n}-S_{n-1}=a_{n}$
Hence; second term

$=4-3=1$
And second term

$-$ first term

$=$ common difference of AP
Therefore, common difference,

$d=1-3=-2$
Now we have the AP as follows
First term,

$\mathrm{a}=3$ Common difference

$=-2$ So AP will look like

$: 3,1, 1,-3,-5$ ,

$\ldots\ldots\ldots$ And, nth term of an AP is given by the formula,

$a_{n}=a+(n-1) d$
Putting the value of a and

$d$ in above formula we get

$\mathrm{a}_{n}=3+(n-1)-2$

$\mathrm{a}_{\mathrm{n}}=3-2 \mathrm{n}+2$

$\mathrm{a}_{\mathrm{n}}=5-2 \mathrm{n}$
So, 3rd term can be can be calculated by just replacing

$n$ with 3

$\mathrm{a}_{3}=5-2 \times 3$

$\mathrm{a}_{3}=-1$
Similarly

$\mathrm{a}_{10}=5-2 \times 10$

$a_{10}=-15$
And so on we can calculate any number of terms of this AP.

12. Find the sum of the first 40 positive integers divisible by 6

Answer

The smallest positive integer which is divisible by 6 is 6 itself and its 40th multiple will be

$6 \times 40=240$
So, we have

$\mathrm{a}=6, \mathrm{~d}=6, \mathrm{n}=40$ and 40th term

$=240$ .
Sum of first 40 positive integers divisible by 6 can be calculated as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$=\frac{40}{2}[2 \times 6+(39) 6]$

$=20(12+234)$

$=20 \times 246$

$=4920$

13. Find the sum of the first 15 multiples of 8.

Answer

As we have to calculate sum of first 15 multiples of 8, series will look like:

$8,16,24, \ldots\ldots\ldots$ up to 15 terms
Given: First term,

$\mathrm{a}=8$ , Common Difference,

$\mathrm{d}=8$ and nth term,

$\mathrm{n}= 15$
Sum of first 15 multiples of 8 can be calculated as:
Sum of n terms of an A.P is given by:

$S_{n}=\frac{N}{2}[2 a+(n-1) d]$
Applying the values from above

$=\frac{15}{2}[2 \times 8+(14) 8]$

$=15(8+56)$

$=15 \times 64=960$
Thus sum of first 15 multiples of 8 is 960.

14. Find the sum of the odd numbers between 0 and 50.

Answer

To Find: Sum of odd numbers from 0 and 50 Let us write these numbers

$1,3,5, \ldots \ldots , 49$
As we can clearly see this forms an AP with first term,

$a=1$ and common difference,

$d=2$ and nth term,

$\mathrm{a}_{\mathrm{n}}= 49$
Now, first we need to find number of terms, for that we have the formula of nth terms of an AP given by

$a_{n}=a+(n-1) d$
Putting the values we get

$49=1+(\mathrm{n}-1) 2$

$48=(\mathrm{n}-1)$

$2(\mathrm{n}-1)=24$

$\mathrm{n}= 25$
So there are 25 odd numbers between 0 and 50 And sum of these 25 numbers are given by using sum of

$S_{n}=\frac{n}{2}[2 a+(n-1) d]$
Putting the values of formula we get,

$S_{25}=\frac{25}{2}[2 \times 1+(25-1) \times 2]$
Terms of an AP

$S_{25}=\frac{25}{2} \times[48+2]$

$S_{25}=25 \times 25$

$S_{25}=625$
So, the sum of odd numbers between 0 and 50 is 625

15. A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs 200 for the first day, Rs 250 for the second day, Rs 300 for the third day, etc., the penalty for each succeeding day being Rs 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days?

Answer

Given:

$\mathrm{a}=200, \mathrm{d}=50$ and

$\mathrm{n}=30$
We can find the penalty by using the sum of 30 terms:

$S=\frac{N}{2}[2 a+(n-1) d]$

$=\frac{30}{2}[2 \times 200+(29) 50]$

$=15(400+1450)$

$=15\times 1850$

$=27750$
Hence, he has to pay an amount of Rs. 27750 as penalty

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Download the Math Ninja App Now

16. A sum of Rs 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.

Answer

As, each price is decreased by 20 rupees, we can consider amount given to each student in increasing order to be an AP.
Let the lowest price given be '

$a$ ' and then prize is increased by Rs 20. In that case, we have First term

$=$ a Common difference,

$d=-20$ No of terms,

$n=$ No of students getting prize

$=7$ Sum of '

$n$ ' terms

$=$ Total prize money

$=700$
Now,
we know, sum of '

$n$ ' terms on AP is

$S=\frac{n}{2}[2 a+(n-1) d]$

$700=\frac{7}{2}[2 \times a+6 \times(-20)]$

$\Rightarrow 700 \times 2=7[2 \mathrm{a}-120]$

$\Rightarrow 200=2 \mathrm{a}-120$

$\Rightarrow 2 \mathrm{a}=200+120$

$\Rightarrow 2 \mathrm{a}= 320$

$\Rightarrow \mathrm{a}=160$
Hence, the divisions are Rs. 160, Rs. 140, Rs. 120, Rs. 100, Rs. 80, Rs. 60, Rs. 40.

17. In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class I will plant 1 tree, a section of Class II will plant 2 trees and so on till Class XII. There are three sections of each class. How many trees will be planted by the students?

Answer

First there are 12 classes and each class has 3 sections
Since each section of class 1 will plant 1 tree, so 3 trees will be planted by 3 sections of class 1. Thus every class will plant 3 times the number of their class
(for example class (iii) will plant

$=3 \times 3=9$ plants)
Similarly,
No. of trees planted by 3 sections of class

$1=3$
No. of trees planted by 3 sections of class

$2=6$
No. of trees planted by 3 sections of class

$3=9$
No. of trees planted by 3 sections of class

$4=12$
Its clearly an AP with first term

$=$ Number of trees planted by class

$1= 3$
We have;

$\mathrm{a}=3, \mathrm{~d}=3$ and

$\mathrm{n}=12$
We can find the total number of trees as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$=\frac{12}{2}[2 \times 3+(11) 3]$

$=6(6+33)$

$=6 \times 39$

$=234$
Total number of trees planted by students

$=234$ .

18. A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii

$0.5 \mathrm{~cm}, 1.0 \mathrm{~cm} ,1.5 \mathrm{~cm}, 2.0 \mathrm{~cm}, \ldots$ as shown in Fig. 5.4. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take

$\pi=\frac{22}{7}$ )

Answer

Circumference of 1st semicircle

$=\pi r=0.5 \pi$
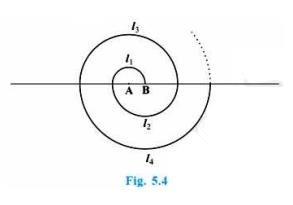
Circumference of 2nd semicircle

$=\pi \mathrm{r}=1 \pi=\pi$
Circumference of 3rd semicircle

$=\pi \mathrm{r}=1.5 \pi$
It is clear that

$\mathrm{a}=0.5 \pi, \mathrm{d}=0.5 \pi$ and

$\mathrm{n}=13$
Hence; the length of the spiral can be calculated as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$=\frac{13}{2}[2 \times 0.5 \pi+(12) \cdot 5 \pi]$

$=\frac{13}{2}[\pi+6 \pi]$

$=\frac{13}{2}(7 \pi)$

$=\frac{13}{2} \times 7 \times \frac{22}{7}$

$=143 \mathrm{~cm}.$

19. 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on (see Fig. 5.5). In how may rows are the 200 logs placed and how many logs are in the top row?

Answer

As, the rows are going up, the no of logs are decreasing,

$20,19,18, \ldots$ , it's an AP Suppose 200 logs are arranged in 'n' rows, then
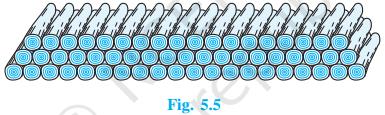
We have; First term,

$a=20$ , Common difference,

$d=-1$ and Sum of

$n$ terms,

$\mathrm{S}_{\mathrm{n}}=$ No of logs

$=200$
We know;

$S=\frac{N}{2}[2 a+(n-1) d]$

$200=\frac{N}{2}[2 \times 20+(N-1)(-1)]$

$400=\mathrm{N}(40-\mathrm{N}+1)$

$400=41 \mathrm{N}-\mathrm{N} 2$

$\mathrm{N}^{2}-41 \mathrm{N}+400=0$

$(\mathrm{N}-16)(\mathrm{N}-25)$
Thus,

$\mathrm{n}=16$ and

$\mathrm{n}=25$
If number of rows is 25 then;

$a_{25}=20+24 \times(-1)$

$=20-24=-4$
Since; negative value for number of logs is not possible hence; number of rows

$=16$

$a_{16}=20+15 \times(-1)$

$=20-15=5$
Thus, number of rows

$=16$ and number of logs in top rows

$=5$

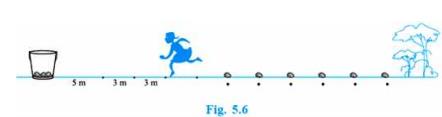
20. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato, and the other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line (see Fig. 5.6).

A competitor starts from the bucket, picks up the nearest potato, runs back with it, deposit in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?

Answer

Distance covered in picking and dropping 1st potato

$=2 \times 5 =10 \mathrm{~m}$
Distance covered in picking and dropping 2nd potato

$=2(5+3)=16 \mathrm{~m}$ Distance covered in picking and dropping 3rd potato

$=2(5+3+3)= 22$ m
Therefore,

$\mathrm{a}=10, \mathrm{~d}=6$ and

$\mathrm{n}=10$
Total distance can be calculated as follows:

$S=\frac{N}{2}[2 a+(n-1) d]$

$=\frac{10}{2}[2 \times 10+(9) 6]$

$=5(20+54)$

$=5 \times 74$

$=370 \mathrm{~m}$
Total distance run by the competitor

$=370 \mathrm{~m}$ .

NCERT Math Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions (English Medium) || CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3

Download the Math Ninja App Now