Class 9 maths chapter 10 exercise 10.6 || class 9 circles exercise10.6 || ncert solutions for class 9 chapter circles exercise 10.6 || exercise 10.6 class 9 maths || circles class 9 exercise 10.6 || exercise 10.6 class 9 || exercise 10.6 class 9 solutions || class 9 exercise 10.6
Explore step-by-step solutions for Class 9 Maths Chapter 10, Exercise 10.6, which further deepens students’ understanding of circle geometry by focusing on practical applications of tangent theorems. This exercise centers around solving problems that involve calculating lengths of tangents, using Pythagoras’ Theorem, and applying key properties such as the fact that tangents from an external point to a circle are equal in length.

class 9 maths chapter 10 exercise 10.6 || class 9 circles exercise 10.6 || ncert solutions for class 9 chapter circles exercise 10.6 || exercise 10.6 class 9 maths || circles class 9 exercise 10.6 || exercise 10.6 class 9 || exercise 10.6 class 9 solutions || class 9 exercise 10.6
Exercise 10.6
1. Prove that the line of centers of two intersecting circles
subtends equal angles at the two points of intersection.
Answer
Let two circles with centers as \(O\) and \( {O}^{\prime}\)
intersect each other at point \(A\) and \(B\) Respectively Join
\(OO^{\prime}\).Now,
In \( \triangle {AOO}^{\prime} \) and \(BOO^{\prime}\)
\(O^{\prime}A = O^{\prime}B\) (radius of same circle)
\( {OA}={OB} \) (Radius of same circle)
\( {OO}^{\prime}={OO}^{\prime} \) (Common)
Hence, by SSS congruence
\( \Delta {OAO}^{\prime} \Delta {OBO} ^{\prime} \)
\( \angle {OAO}^{\prime}=\angle {OBO}^{\prime} \) (By CPCT)
Therefore,
Line of centers of two intersecting circles subtends equal angles at the two points of intersection.
2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of
a circle are parallel to each other and are on opposite sides of
its centre. If the distance between \( A B \) and \( C D \) is 6
cm, find the radius of the circle.
Answer
Draw OM perpendicular AB and ON perpendicular CD Join OB and OD
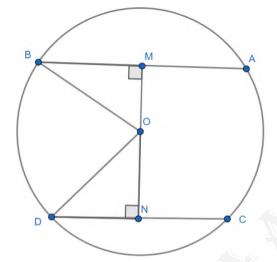
\( {BM}= \) (The perpendicular drawn from the center bisects the chord)
Let ON be \(x\)
Therefore, OM will be \( 6-{x} \)
In \( \triangle {MOD} \),
\({OM}^{2}+{MB}^{2}={OB}^{2}\)
\((6-{x})^{2}+2={OB}^{2}\)
\(36+{x}^{2}-12 {x}+{OB}^{2} \quad \ldots\ldots\text{(i)}\)
In \( \triangle {NOD} \),
\({ON}^{2}+{ND}^{2}={OD}^{2}\)
\(({x})^{2}+\left(\frac{11}{2}\right)^{2}={OD}^{2}\)
\(({x})^{2}+\frac{121}{4}={OD}^{2}\quad \ldots\ldots\text{(ii)}\)
We have \(OB = OD\) (radii of the same circle)
Therefore,
From (i) and (ii),
\(36+x^{2}-12 x+\frac{25}{4}=(x)^{2}+\frac{121}{2}\)
\(36-12 x+\frac{25}{4}=\frac{121}{2}\)
\(x=1\)
From (ii),
\( (1)^{2}+\frac{121}{4}={OD}^{2} \)
\( {OD}=\frac{5}{2} \sqrt{5} \text{ cm} \)
3. The lengths of two parallel chords of a circle are 6 cm and 8
cm. If the smaller chord is at distance 4 cm from the centre, what
is the distance of the other chord from the centre?
Answer
Let AB and CD be two parallel chords in a circle centered at O
Join OB and ODDistance of the smaller chord AB from the centre of the circle \( =4 {~cm} \)
\( {OM}=4 {~cm} \)
\( {MB}=\frac{A B}{2}=\frac{6}{2}=3 {~cm} \).
In \( \triangle {OMB} \),
\({OM}^{2}+{MB}^{2}={OB}^{2}\)
\((4)^{2}+2={OB}^{2}\)
\(16+9={OB}^{2}\)
\({OB}=5 {~cm}\)
In \( \triangle {OND} \),
\({ON}^{2}+{ND}^{2}={OD}^{2}\)
\(({ON})^{2}+2=5^{2}\)
\(({ON})^{2}=9\)
\({ON}=3 {~cm}\)
4. Let the vertex of an angle ABC be located outside a circle and
let the sides of the angle intersect equal chords AD and CE with
the circle. Prove that \( \angle {ABC} \) is equal to half the
difference of the angles subtended by the chords AC and DE at the
centre.
Answer
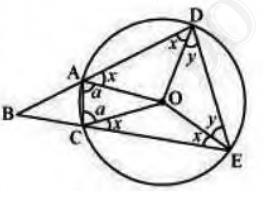
In \( \triangle {AOD} \) and \( \triangle {COE} \),
\( {OA}={OC} \) (radii)
\( {OD}={OE} \) (Radii)
\( {AD}={CE} \) (Given)
Therefore,
By SSS congruence,
\( \triangle {AOD} \Delta {COE} \)
\( \angle {OAD}=\angle {OCE} \ (\text{By CPCT}) \quad \ldots\ldots\text{(i)}\)
\( \angle O D A=\angle O E C \ (\text{By CPCT}) \quad \ldots\ldots\text{(ii)}\)
\( \angle {OAD}=\angle {ODA} \quad \ldots\ldots\text{(iii)}\)
Using (i), (ii) and (iii), we get
\(\angle {OAD}=\angle {OCE}=\angle {ODA}=\angle {OEC}={x}\)
Now,
In triangle \(ODE\),
\({OD}={OE}\)
Hence, ABCD is a quadrilateral
\(\angle {CAD}+\angle {DEC}=180^{\circ}\)
\({a}+{x}+{x}+{y}=180^{\circ}\)
\(2 {x}+{a}+{y}=180^{\circ}\quad \ldots\ldots\text{(iv)}\)
\(\angle {DOE}=180^{\circ}-2 {y}\)
And,
\(\angle {COA}=180^{\circ}-2 {a}\)
\(\angle {DOE}-\angle {COA}=2 {a}-2 {y}\)
\(=2 {a}-2\left(180^{\circ}-2 {x}-{a}\right)\)
\(=4 {a}+4 {x}-360^{\circ}\quad \ldots\ldots\text{(v}\)
\(\angle B A C=180^{\circ}-({a}+{x})\)
And
\(\angle {ACB}=180-({a}-{x})\)
In \( \triangle {ABC} \),
\(\angle {ABC}+\angle {BAC}+\angle {ACB}=180^{\circ} \ (\text {Angle sum property of triangle})\)
\(\angle {ABC}=2 {a}+2 {x}-180^{\circ}\)
\(\angle {ABC}=\frac{ 1 }{ 2 }(4 {a}+{ax}-3600)\quad[\text {using (v)}]\)
5. Prove that the circle drawn with any side of a rhombus as
diameter, passes through the point of intersection of its
diagonals.
Answer
Let ABCD be a rhombus in which diagonals intersect at point O and
a circle is drawn is drawn taking side CD as diameterNow,
\(\angle C O D=90^{\circ}\) (Since, diagonals of rhombus intersect at \( 90^{\circ} \))
Hence,
\(\angle {AOB}=\angle {BOC}=\angle {COD}=\angle {DOA}=90^{\circ}\)
Hence, point O has to lie on the circle
6. ABCD is a parallelogram. The circle through A, B and C
intersect CD (produced if necessary) at \( E \). Prove that \(
{AE}={AD} \).
Answer
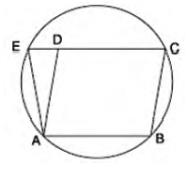
It is visible that ABCE is a cyclic quadrilateral and in a cyclic quadrilateral, the sum of opposite angle is \( 180^{\circ} \).
\(\angle {AEC}=\angle {CBA}=180\)
\(\angle {AED}=\angle {CBA}\quad \ldots\ldots\text{(i)}\)
We know that: Opposite angles of a parallelogram are equal
Hence,
\(\angle {ADE}=\angle {CBA} \quad \ldots\ldots\text{(ii)}\)
Using (i) and (ii)
\(\angle {ADE}=\angle {AED}\)
\( {AE}={AD} \) (angles opposite to equal sides are equal)
class 9 maths chapter 10 exercise 10.6 || class 9 circles exercise 10.6 || ncert solutions for class 9 chapter circles exercise 10.6 || exercise 10.6 class 9 maths || circles class 9 exercise 10.6 || exercise 10.6 class 9 || exercise 10.6 class 9 solutions || class 9 exercise 10.6
7. AC and BD are chords of a circle which bisect each other.
Prove that:
(i) AC and BD are diameters
(ii) ABCD is a rectangle.
(i) AC and BD are diameters
(ii) ABCD is a rectangle.
Answer
Let two chords AB and CD are intersecting each other at point O
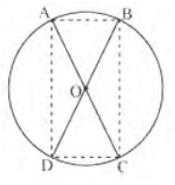
In \( \triangle {AOB} \) and \( \triangle {COD} \),
\( {OA}={OC} \) (Given)
\( {OB}={OD} \) (Given)
\( \angle {AOB}=\angle {COD} \) (Vertically opposite angles)
\( \triangle {AOB} \triangle {COD} \) (SAS congruence rule)
\( {AB}={CD}\text{ (By CPCT)} \)
Similarly, it can be proved that \( \triangle {AOD} \triangle {COB} \)
\( {AD}={CB} \) (By CPCT)
Since in quadrilateral \( A C B D \), opposite sides are equal in length, \( A C B D \) is a parallelogram
\(\angle {A}=\angle {C}\)
However,
\(\angle {A}+\angle {C}=180^{\circ} \ ({ABCD} \text { is a cyclic quadrilateral})\)
\(\angle {A}+\angle {A}=180^{\circ}\)
\(2 \angle {A}=180^{\circ}\)
\(\angle {A}=90^{\circ}\)
As ACBD is a parallelogram and one of its interior angles is \( 90^{\circ} \), therefore, it is a rectangle
\( A \) is the angle subtended by chord \( B D \) and \( B D \) should be the diameter of the circle
Similarly, AC is the diameter of the circle
8. Bisectors of angles \( {A}, {B} \), and \(C\) of a triangle
\(ABC\) intersect its circumcircle at \( {D}, {E} \) and \(F\)
respectively. Prove that the angles of the triangle \(DEF\) are \(
90^{\circ}-\frac{1}{2} A, 90^{\circ}-\frac{1}{2} B \) and \(
90^{\circ}-\frac{1}{2} C \).
Answer
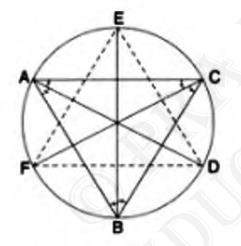
It is given in the question that,
\( \angle {ABE}=\frac{B}{2} \)
However,
\( \frac{B}{2}=\angle {ADE} \)
Like this, similarly
\( \angle {ACF}=\angle {ADF}=\frac{C}{2} \)
\( {D}=\angle {ADE}+\angle {ADF} \)
\(=\frac{B}{2}+\frac{C}{2}\)
\(=\frac{1}{2}(\angle {B}+\angle {C})\)
\(=\frac{1}{2}\left(180^{\circ}-\angle {A}\right)\)
\(=90^{\circ}-\angle {A}\)
Similarly,
\(E=90^{\circ}-\angle B\)
And,
\({F}=90^{\circ}-\frac{1}{2} \angle {C}\)
9. Two congruent circles intersect each other at points A and B.
Through \( A \) any line segment PAQ is drawn so that \( {P}, {Q}
\) lie on the two circles. Prove that \( {BP}={BQ} \).
Answer
\( A B \) is common chord in the given both circles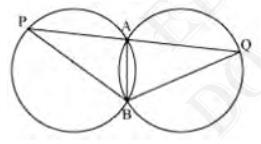
Also, circles are congruent
So,
\(\angle {APB}=\angle {AQB}\)
Now, in triangle \(BPQ \)
\( \angle {APB}=\angle {AQB} \)
\( {BQ}={BP} \) (Angles opposite to equal sides are equal)
10. In any triangle \(ABC \), if the angle bisector of \( \angle
{A} \) and perpendicular bisector of \(BC\) intersect, prove that
they intersect on the circum circle of the triangle \( A B C
\).
Answer
Let perpendicular bisector of side BC and angle bisector of A meet
at point D. Let the perpendicular bisector of side BC intersect it
at E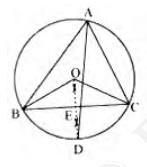
Perpendicular bisector of side BC will pass through circum centre O of the circle
BOC and BAC are the angles subtended by arc BC at the centre and a point \( A \) on the remaining part of the circle respectively
\( \angle {BOC}=2 \angle {BAC}=2 \angle {A}\quad \ldots\ldots\text{(i)} \)
In \( \triangle {BOE} \) and \( \triangle {COE} \),
\( {OE}={OE} \) (Common)
\( {OB}={OC} \) (Radii of same circle)
\( \angle {OEB}=\angle {OEC}\) (Each \( 90^{\circ} \) as OD perpendicular to BC)
\( \triangle {BOE} \cong \Delta {COE} \) (RHS congruence rule)
\( \angle {BOE}=\angle {COE} \) (By CPCT) \(\quad \ldots\ldots\text{(ii)}\)
However,
\(\angle {BOE}+\angle {COE}=\angle {BOC}\)
\(\angle {BOE}+\angle {BOE}=2 \angle {A}\quad[\text {From (i) and (ii)}]\)
\(2 \angle {BOE}=2 \angle {A}\)
\(\angle {BOE}=\angle {A}\)
\(\angle {BOE}=\angle {COE}=\angle {A}\)
The perpendicular bisector of side \(BC\) and angle bisector of \(A\) meet at point \( D \)
\(\angle {BOD}=\angle {BOE}=\angle {A} \quad \ldots\ldots\text{(iii)}\)
Since \( A D \) is the bisector of angle \( A \)
\(\angle {BAD}=\frac{A}{2}\)
\(2 \angle {BAD}={A} \quad \ldots\ldots\text{(iv)}\)
From (iii) and (iv), we get
\(\angle {BOD}=2 \angle {BAD}\)
Hence, proved.

