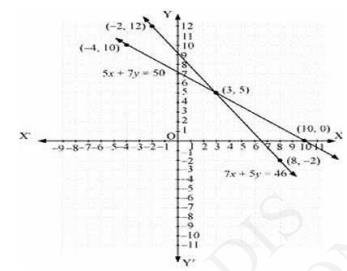
3.
(i) On comparing the ratios \( \frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}} \) and \( \frac{c_{1}}{c_{2}} \) find out whether the following pair of linear equations are consistent, or inconsistent.
\( \quad 3 x+2 y=5 ; 2 x-3 y=7 \)
\( \quad 3 x+2 y=5 ; 2 x-3 y=7 \)
Answer
We get\(=\frac{a_{1}}{a_{2}}=\frac{3}{2}\)
\(=\frac{b_{1}}{b_{2}}=-\frac{2}{3}\)
Hence,
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
Therefore, these linear equations will intersect at one point only and have only one possible solution and pair of linear equations is inconsistent.
(ii) On comparing the ratios \( \frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}} \) and \( \frac{c_{1}}{c_{2}} \) find out whether the following pair of linear equations are consistent, or inconsistent.
\( \quad 2 \mathrm{x}-3 \mathrm{y}=8 ; 4 \mathrm{x}-6 \mathrm{y}=9 \)
\( \quad 2 \mathrm{x}-3 \mathrm{y}=8 ; 4 \mathrm{x}-6 \mathrm{y}=9 \)
Answer
We get,\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\)
\(=\frac{b_{1}}{b_{2}}=\frac{-3}{-6}=\frac{1}{2}\)
\(=\frac{c_{1}}{c_{2}}=\frac{8}{9}\)
Hence,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Therefore, these linear equations are parallel to each other and have no possible solution.
And pair of linear equations is inconsistent.
(iii) On comparing the ratios \( \frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}} \) and \( \frac{c_{1}}{c_{2}} \) find out whether the following pair of linear equations are consistent, or inconsistent.
\( \frac{3}{2} x+\frac{5}{3} y=7 ; 9 x-10 y=14 \)
\( \frac{3}{2} x+\frac{5}{3} y=7 ; 9 x-10 y=14 \)
Answer
\( \frac{3}{2} x+\frac{5}{3} y=7 \)\( 9 x-10 y=14 \)
We get,
\(\frac{a_{1}}{a_{2}}=\frac{\frac{3}{2}}{9}=\frac{3}{18}=\frac{1}{6}\)
\(\frac{b_{1}}{b_{2}}=\frac{\frac{5}{3}}{-10}=\frac{5}{-30}=-\frac{1}{6}\)
\(=\frac{c_{1}}{c_{2}}=\frac{7}{14}=\frac{1}{2}\)
Hence,
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
Therefore, these linear equations will intersect each other at one point and have only one possible solution.
And, the pair of linear equations is consistent.
(iv) On comparing the ratios \( \frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}} \) and \( \frac{c_{1}}{c_{2}} \) find out whether the following pair of linear equations are consistent, or inconsistent.
\( 5 x-3 y=11 ;-10 x+6 y=-22 \)
\( 5 x-3 y=11 ;-10 x+6 y=-22 \)
Answer
We get\(=\frac{a_{1}}{a_{2}}=\frac{5}{-10}=-\frac{1}{2}\)
\(=\frac{b_{1}}{b_{2}}=-\frac{3}{6}=-\frac{1}{2}\)
\(=\frac{c_{1}}{c_{2}}=\frac{11}{-22}=-\frac{1}{2}\)
Hence,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Therefore these pair of lines has the infinite number of solutions. and pair of linear equations is inconsistent
(v) On comparing the ratios \( \frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}} \) and \( \frac{c_{1}}{c_{2}} \) find out whether the following pair of linear equations are consistent, or inconsistent.
\( \frac{4}{3} x+2 \mathrm{y}=8 ; 2 \mathrm{x}+3 \mathrm{y}=12 \)
\( \frac{4}{3} x+2 \mathrm{y}=8 ; 2 \mathrm{x}+3 \mathrm{y}=12 \)
Answer
We get\(=\frac{a_{1}}{a_{2}}=\frac{4}{6}=\frac{2}{3}\)
\(=\frac{b_{1}}{b_{2}}=\frac{2}{3}\)
\(=\frac{c_{1}}{c_{2}}=\frac{8}{12}=\frac{2}{3}\)
Hence,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Therefore these pair of lines have infinite number of solutions and pair of linear equation is consistent.
CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2

4.
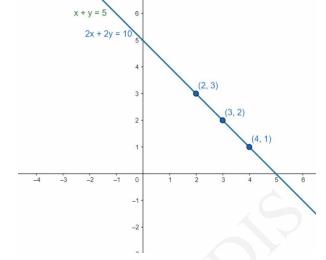
(i) Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
\( x+y=5 ; 2 x+2 y=10 \)
\( x+y=5 ; 2 x+2 y=10 \)
Answer
We get\(\frac{a_{1}}{a_{2}}=\frac{1}{2}\)
\(\frac{b_{1}}{b_{2}}=\frac{1}{2}\)
\(\frac{c_{1}}{c_{2}}=\frac{5}{10}=\frac{1}{2}\)
Hence,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
\(\mathrm{x}+\mathrm{y}=5\)
\(\mathrm{x}=5-\mathrm{y}\)
Putting \( \mathrm{y}=1,2,3 \) we get
\(x=5-1=4\)
\(x=5-2=3\)
\(x=5-3=2\)
\(\begin{array}{|l|l|l|l|}
\hline X & 4 & 3 & 2 \\\hline Y & 1 & 2 & 3 \\\hline\end{array}\)
And, \( 2 \mathrm{x}+2 \mathrm{y}=10 \)
\(X=\frac{10-2 y}{2} \)
\(\begin{array}{|l|l|l|l|}
\hline X & 4 & 3 & 2 \\\hline Y & 1 & 2 & 3 \\\hline\end{array}\)
(ii) Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
\( x-y=8,3 x-3 y=16 \)
\( x-y=8,3 x-3 y=16 \)
Answer
We get\(\frac{a_{1}}{a_{2}}=\frac{1}{3}\)
\( \frac{b_{1}}{b_{2}}=\frac{-1}{-3}=\frac{1}{3} \)
\(\frac{c_{1}}{c_{2}}=\frac{8}{16}=\frac{1}{2}\)
Hence,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Therefore, these linear equations are parallel to each other and have no possible solution,
Hence, the pair of linear equations is inconsistent.
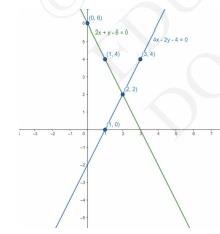
(iii) Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
\( 2 x+y-6=0,4 x-2 y-4=0 \)
\( 2 x+y-6=0,4 x-2 y-4=0 \)
Answer
We get,\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\)
\(\frac{b_{1}}{b_{2}}=\frac{1}{-2}\)
\(\frac{c_{1}}{c_{2}}=\frac{-6}{-4}=\frac{3}{2}\)
Hence,
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution.
Hence, pair of linear equations is consistent.
\(2 x+y-6=0\)
\(=y=6-2 x\)
\(\begin{array}{|l|l|l|l|}
\hline X & 0 & 1 & 2 \\\hline Y & 6 & 4 & 2 \\\hline\end{array}\)
And, \( 4 \mathrm{x}-2 \mathrm{y}-4=0 \)
\(=y=\frac{4 x-4}{2}\)
\(\begin{array}{|l|l|l|l|}\hline X & 1 & 2 & 3 \\\hline Y & 0 & 2 & 4 \\\hline\end{array}\)
Graphical representation
(iv) Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
\( 2 x-2 y-2=0,4 x-4 y-5=0 \)
\( 2 x-2 y-2=0,4 x-4 y-5=0 \)
Answer
We get, \(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\)
\(\frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2}\)
\(\frac{c_{1}}{c_{2}}=\frac{2}{5} s\)
Hence,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Therefore, these linear equations are parallel to each other and have no possible solution,
Hence, the pair of linear equations is inconsistent.
5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m . Find the dimensions of the garden.
Answer
Let the length and breadth of garden be ' \( x \) ' and ' \( y \) ' respectively. Given, Half the perimeter is 36 m We know perimeter of Rectangle \( = \) \( 2( \) length + breadth) Half the perimeter \( =x+y \Rightarrow x+y=36 \Rightarrow x=36 - y [1]\) Also, Length is 4 m more than width \( \Rightarrow \mathrm{x}=\mathrm{y}+4 [2]\) From [1] and [2], we have \( 36-\mathrm{y}=\mathrm{y}+4 \Rightarrow 2 \mathrm{y}=32 \Rightarrow \mathrm{y}=16 \) Putting in [1], we have \( \Rightarrow \mathrm{x}=36-16=20 \) Hence, Length and Breadth of garden are 20 m and 16 m respectively.
6.
(i) Given the linear equation \( 2 x+3 y-8=0 \), write another linear equation in two variables such that the geometrical representation of the pair so formed is:
Intersecting lines
Intersecting lines
Answer
Intersecting lines: For this condition, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
The second line such that it is intersecting the given line is
\(2 x+4 y-6=0\)
As
\(\frac{a_{1}}{a_{2}}=\frac{2}{2}=1\)
\(\frac{b_{1}}{b_{2}}=\frac{3}{4} \text { and } \frac{a_{1}}{a_{2}} \neq\frac{b_{1}}{b_{2}}\)
(ii) Given the linear equation \( 2 x+3 y-8=0 \), write another linear equation in two variables such that the geometrical representation of the pair so formed is:
Parallel lines
Parallel lines
Answer
Parallel lines:For this condition
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, the second line can be \( 4 x+6 y-8=0 \)
As \( \frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2} \),
\( \frac{b_{1}}{b_{2}}=\frac{3}{6}=\frac{1}{2} \)
\(\frac{c_{1}}{c_{2}}=\frac{-8}{-8}=1\)
So, \( \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \)
(iii) Given the linear equation \( 2 x+3 y-8=0 \), write another linear equation in two variables such that the geometrical representation of the pair so formed is:
Coincident lines
Coincident lines
Answer
Coincident lines: For coincident lines,\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence,
the second line can be \( 6 x+9 y-24=0 \)
\(\frac{a_{1}}{a_{2}}=\frac{2}{6}=\frac{1}{3}\)
\(\frac{b_{1}}{b_{2}}=\frac{3}{9}=\frac{1}{3}\)
\(\frac{c_{1}}{c_{2}}=\frac{-8}{-24}=\frac{1}{3}\)
So,
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
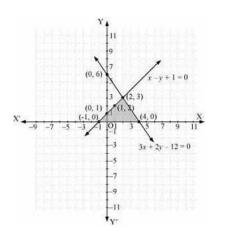
7. Draw the graphs of the equations \( x-y+1=0 \) and \( 3 x+2 y-12= \) 0 . Determine the coordinates of the vertices of the triangle formed by these lines and the \( x \)-axis, and shade the triangular region.
Answer
Equation: 1\(x-y+1=0\)
\(x=y-1\)
Let us find the coordinates satisfying the above equation,
\(\begin{array}{|l|l|l|l|l|}
\hline X & 0 & 1 & 2 & -1 \\\hline Y & 1 & 2 & 3 & 0 \\\hline \end{array}\)
Equation 2:
\(3 x+2 y-12=0\)
\(x=\frac{12-2 y}{3}\)
\(\begin{array}{|l|l|l|l|}
\hline X & 4 & 2 & 0 \\
\hline Y & 0 & 3 & 6 \\
\hline
\end{array}\)
By taking, coordinates we can plot the both equations in graph.
Hence, the graphic representation is as follows.
CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2
Central Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.3