(iv) Solve the following pair of linear equations.
\( (a-b) x+(a+b) y=a^{2}-2 a b-b^{2} \)
\(
(a+b)(x+y)=a^{2}+b^{2}
\)
\( (a-b) x+(a+b) y=a^{2}-2 a b-b^{2} \)
\(
(a+b)(x+y)=a^{2}+b^{2}
\)
Answer
\((a-b) x+(a+b) y=a^{2}-2 a b-b^{2}\ldots(1)\)\((a+b)(x+y)=a^{2}+b^{2}\)
\((a+b) x+(a+b) y=a^{2}+b^{2} \ldots(2)\)
Subtracting equation (2) from (1), we obtain
\((a-b) x-(a+b) x=\left(a^{2}-2 a b-b^{2}\right)\left(a^{2}+b^{2}\right)(a-b-a-b) x=-2 a b-2 b^{2}\)
\(-2 b x=-2 b(a+b)\)
\(x=a+b\)
Using equation (1), and putting the value of \( x \) in the equation we obtain
\((a-b)(a+b)+(a+b) y=a^{2}-2 a b-b^{2} a^{2}-b^{2}+(a+b) y=a^{2}-2 a b-b^{2}\)
\((a+b) y=-2 a b\)
\(y=\frac{-2 a b}{a+b}\)
(v) Solve the following pair of linear equations.
\( 152 x-378 y=-74 \)
\(
-378 x+152 y=-604
\)
\( 152 x-378 y=-74 \)
\(
-378 x+152 y=-604
\)
Answer
\( 152 x-378 y=-74 \ldots(1)\)\(
-378 x+152 y=-604\ldots(2)\)
Multiply eq (2) by 152 and equation (1) by 378
\(378 \times 152 x-3782 y=-74 \times 378\)
\(-378 \times 152 x+1522 y=-604 \times 152\)
Adding both the questions we get
\(\left(152^{2}-378^{2}\right) y=-119780\)
\(-119780 y=-119780\)
\(y=1\)
put the value in eq 1 ,
\( 152 \mathrm{x}-378 \times 1=-74152 \mathrm{x}=378-74152 \mathrm{x}=304 \mathrm{x}=2 \) we get \( \mathrm{x}=2 \).
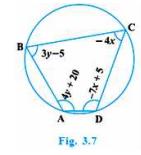
8. ABCD is a cyclic quadrilateral (see Fig. 3.7). Find the angles of the cyclic quadrilateral.

Answer
We know that the sum of the measures of opposite angles in a cyclic quadrilateral is \( 180^{\circ} \). Therefore, \( \angle \mathrm{A}+\angle \mathrm{C}=180 \)\(\Rightarrow 4 y+20-4 x=180\)
\(\Rightarrow-4 x+4 y=160\)
\(\Rightarrow x-y=-40 \ldots (i)\)
Also, \( \angle \mathrm{B}+\angle \mathrm{D}=180 \)
\(\Rightarrow 3 y-5-7 x+5=180\)
\(\Rightarrow-7 x+3 y=180\ldots(ii)\)
Multiplying equation (i) by 3 , we obtain
\( 3 x-3 y=-120 \ldots(iii) \)
Adding equations (ii) and (iii), we obtain
\(-7 x+3 x=180-120\)
\(-4 x=60\)
\(x=-15\)
By using equation (i), we obtain \( x-y=-40 \)
\(-15-y=-40\)
\(y=-15+40\)
\(=25\)
\( \angle \mathrm{A}=4 \mathrm{y}+20\)
\(=4(25)+20 \angle \mathrm{A}=120^{\circ}\)
\(\angle \mathrm{B}=3 \mathrm{y}-5\)
\(=3(25)-5 \angle \mathrm{B}=70^{\circ}\)
\(\angle \mathrm{C}=-4 \mathrm{x}\)
\(=-4(-15)\)
\(\angle \mathrm{C}=60^{\circ}\)
\(\angle \mathrm{D}=-7 \mathrm{x}+5 \)
\(=-7(-15)+5\)
\(=105+5\)
\(\angle \mathrm{D}=110^{\circ} \)
NCERT Solutions for Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.7 Math Solution
Download the Math Ninja App NowCentral Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.3
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.4
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.5
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.6
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2