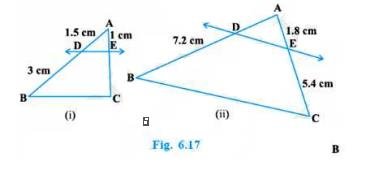
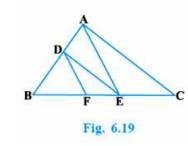
4. In Fig. 6.19, DE \( \| \mathrm{AC} \) and \( \mathrm{DF} \| \mathrm{AE} \). Prove that
\(\frac{B F}{F E}=\frac{B E}{E C}\)

\(\frac{B F}{F E}=\frac{B E}{E C}\)
Answer
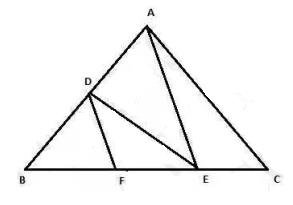
To Prove \( \frac{B F}{F E}=\frac{B E}{E C} \)
Given:
Basic Proportionality Theorem: If a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion. In triangle \( \mathrm{ABC}, \mathrm{DE} \) is parallel to AC
Therefore,
By Basic proportionality theorem
\( \frac{B F}{F E}=\frac{B E}{E C} \quad\ldots \text{(1)}\)
In triangle \( \mathrm{BAE}, \mathrm{DF} \) is parallel to AE
In triangle \( \mathrm{BAE}, \mathrm{DF} \) is parallel to AE
Therefore, By Basic proportionality theorem
\( \frac{B D}{D A}=\frac{B F}{F E}\quad\ldots \text{(2)} \)
From (1) and (2), we get
\( \frac{B E}{E C}=\frac{B F}{F E} \)
Hence, Proved.
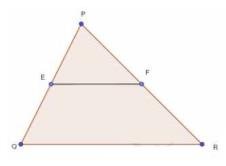
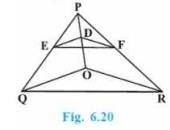
5. In Fig. 6.20, \(DE \| OQ\) and \( \mathrm{DF} \| OR\). Show that \( E F \| \) QR.

Answer
To Prove: \(EF \| QR\)Given: In triangle POQ, DE parallel to OQ Proof:
In triangle \( \mathrm{POQ}, \mathrm{DE} \) parallel to OQ
Hence,
Basic Proportionality Theorem: If a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.
\( \frac{P E}{E q}=\frac{P D}{D O} \quad \) (Basic proportionality theorem) (i)
Now,
In triangle POR, DF parallel OR
Hence,
\( \frac{P F}{F R}=\frac{P D}{D O} \quad \) (Basic proportionality theorem) (ii)
From (i) and (ii), we get
\( \frac{P E}{E Q}=\frac{P F}{F R} \)
Therefore,
EF is parallel to QR (Converse of basic proportionality theorem)
Hence, Proved.
NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.2
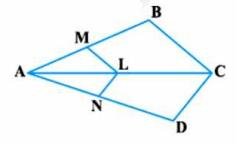
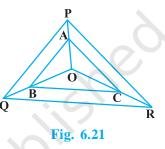
Download the Math Ninja App Now6. In Fig. 6.21, A, B and C are points on \( \mathrm{OP}, \mathrm{OQ} \) and OR respectively such that \( A B \| P Q \) and \( A C \| P R \). Show that \( B C \| Q R \).

Answer
To Prove: \(BC || QR\)Given that in triangle \( \mathrm{POQ}, \mathrm{AB} \) parallel to PQ
Hence,
Basic Proportionality Theorem: If a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.
\( \frac{O A}{A P}=\frac{O B}{B Q} \ ( \)Basic proportionality theorem \( ) \)
Now,
Therefore,
Basic Proportionality Theorem: If a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.
Using Basic proportionality theorem, we get:
\( \frac{O A}{A P}=\frac{O C}{C R} \)
From above equations, we get
\( \frac{O B}{B Q}=\frac{O C}{C R} \)
BC is parallel to QR (By the converse of Basic proportionality theorem)
Hence, Proved.
7. Using Theorem 6.1, prove that a line drawn through the midpoint of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX)
Answer
Consider the given figure in which PQ is a line segment drawn through the mid-point \( P \) of line \( A B \), such that \( P Q \) is parallel to BC.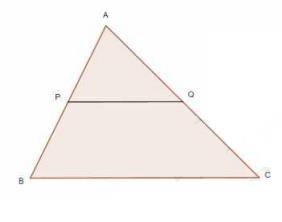
To Prove: PQ bisects AC
Given: \( P Q || \mathrm{BC} \) and PQ bisects AB
Proof:
According to Theorem 6.1 : If a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion. Now, using basic proportionality theorem, we get
\(\frac{A Q}{Q C}=\frac{A P}{P B}\)
\(\frac{A Q}{Q C}=\frac{1}{1} \)
[As \( \mathrm{AP}=\mathrm{PB} \operatorname{coz} \mathrm{P} \) is the mid-point of AB ]
Hence,
\( \mathrm{AQ}=\mathrm{QC} \)
Or, Q is the mid-point of AC
Hence proved.
8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX)
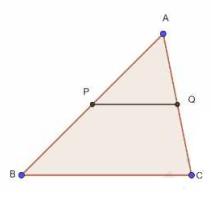

Answer
To Prove: \( P Q \| B C \)Given: \( P \) and \( Q \) are midpoints of \( A B \) and \( A C \)
Proof:
Let us take the given figure in which PQ is a line segment which joins the mid-points P and Q of line AB and AC respectively
i.e., \( \mathrm{AP}=\mathrm{PB} \) and \( \mathrm{AQ}=\mathrm{QC} \)
We observe that,
\( \frac{A P}{P B}=\frac{1}{1} \)
And,
\( \frac{A Q}{Q C}=\frac{1}{1} \)
Therefore,
\( \frac{A P}{P B}=\frac{A Q}{Q C} \)
Basic Proportionality Theorem: If a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.
Hence, using basic proportionality theorem we get:
PQ parallel to BC
Hence, Proved.
NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.2
Download the Math Ninja App Now9. ABCD is a trapezium in which \( \mathrm{AB} \| \mathrm{DC} \) and its diagonals intersect each other at the point O. Show that \( \frac{A O}{B O}=\frac{C O}{D O} \).
Answer
The figure is given below: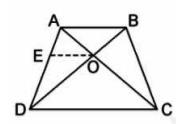
Given: \( A B C D \) is a trapezium
\( \mathrm{AB} \| \mathrm{CD} \)
Diagonals intersect at O
To Prove \( =\frac{A O}{B O}=\frac{C O}{D O} \)
Construction: Construct a line EF through point O, such that EF is parallel to CD.
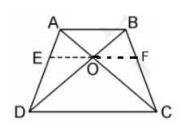
Proof:
In \( \triangle \mathrm{ADC}, \mathrm{EO} \) is parallel to CD
According to basic proportionality theorem, if a side is drawn parallel to any side of the triangle then the corresponding sides formed are proportional.
Now, using basic proportionality theorem in \( \triangle \mathrm{ABD} \) and \( \triangle \mathrm{ADC} \), we obtain
\( \frac{A E}{E D}=\frac{A O}{O C} \quad\ldots \text{(i)}\)
In \( \triangle \mathrm{ABD}, \mathrm{OE} \) is parallel to AB
So, using basic proportionality theorem in \( \triangle \mathrm{EOD} \) and \( \triangle \mathrm{ABD} \), we get
\( \frac{E D}{A E}=\frac{O D}{B O} \)
\( \frac{A E}{E D}=\frac{B O}{O D}\quad\ldots \text{(ii)} \)
From (i) and (ii), we get
\( \frac{A O}{O C}=\frac{B O}{O D} \)
Therefore by cross multiplying we get,
\( \frac{A O}{B O}=\frac{O C}{O D} \)
Hence, Proved.
10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that \( \frac{A O}{B O}=\frac{C O}{D O} \). Show that ABCD is a trapezium
Answer
The quadrilateral ABCD is shown below, BD and AC are the diagonals.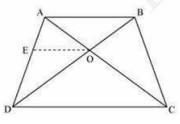
Construction: Draw a line OE parallel to AB
Given: In \( \triangle \mathrm{ABD}, \mathrm{OE} \) is parallel to AB
To prove: \( A B C D \) is a trapezium
According to basic proportionality theorem, if in a triangle another line is drawn parallel to any side of triangle, then the sides so obtain are proportional to each other.
Now, using basic proportionality theorem in \( \triangle \mathrm{DOE} \) and \( \triangle \mathrm{ABD} \), we obtain
\( \frac{A E}{E D}=\frac{B O}{O D} \quad\ldots \text{(i)}\)
It is given that,
\( \frac{A O}{O C}=\frac{O B}{O D} \quad\ldots \text{(ii)}\)
From (i) and (ii), we get
\( \frac{A E}{E D}=\frac{A O}{O C} \quad\ldots \text{(iii)}\)
Now for \( A B C D \) to be a trapezium \( A B \) has to be parallel of \( C D \)
Now From the figure we can see that If eq(iii) exists then,
\(EO || DC\) (By the converse of basic proportionality theorem)
Now if,
\( \Rightarrow \mathrm{AB}\|\mathrm{OE}\| \mathrm{DC} \)
Then it is clear that
\( \Rightarrow \mathrm{AB} \| \mathrm{CD} \)
Thus the opposite sides are parallel and therefore it is a trapezium.
Hence,
ABCD is a trapezium.
NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.2
Download the Math Ninja App NowCentral Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.3
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.4
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.5
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.6
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2