CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Explore the NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium), with detailed explanations for Exercise 4.2. This resource is designed to simplify complex Quadratic Equations, helping Class 10 Maths students grasp the subject effortlessly. For any queries regarding NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2, feel free to leave a comment, and we’ll respond as soon as possible.

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)
Exercise 4.2

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now

1. Find the roots of the following quadratic equations by factorisation:

(i) $ x^{2}-3 x-10=0 $

Answer

$ X^{2}-3 x-10 $
$=x^{2}-5 x+2 x-10$
$=x(x-5)+2(x-5)$
$=(x-5)(x+2)$
Roots of this equation are the values for which $ (x-5)(x+2)=0 $
$ \therefore \mathrm{x}-5=0 $ or $ \mathrm{x}+2=0 $
i.e., $ x=5 $ or $ x=-2 $

(ii) $ 2 x^{2} +x -6=0 $

Answer

$2 x^{2}+x-6$
$=2 x^{2}+4 x-3 x-6$
$=2 x(x+2)-3(x+2)$
$=(x+2)(2 x-3)$
Roots of this equation are the values for which $ (x+2)(2 x-3)=0 $
$ \therefore \mathrm{x}+2=0 $ or $ 2 \mathrm{x}-3=0 $
$ x=-2 $ or $ x=\frac{3}{2} $

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now

(iii) $ \sqrt{2} x^{2}+7 x+5 \sqrt{2} $

Answer

$ \sqrt{2} x^{2}+7 x+5 \sqrt{2} $
$\sqrt{2} x^{2}+5 x+2 x+5 \sqrt{2}$
$=x(\sqrt{2} x+5)+\sqrt{2}(\sqrt{2} x+5)$
$(\sqrt{2} x+5)(x+\sqrt{2})$
Roots of this equation are the values for which $ (\sqrt{2} x+5)(x+\sqrt{2})=0 $
$\sqrt{2} x+5=0 \text { or } x+\sqrt{2}=0$
$x=\frac{-5}{\sqrt{2} x}, x=-\sqrt{2}$

(iv) $ 2 x^{2}-x+\frac{1}{8}=0 $

Answer

$\text { (iv) } 2 x^{2}-x+\frac{1}{8}=0$
$=\frac{1}{8}\left(16 x^{2}-8 x+1\right)$
$=\frac{1}{8}\left(16 x^{2}-4 x-4 x+1\right)$
$=\frac{1}{8}(4 x(4 x-1)-1(4 x-1))$
$=\frac{1}{8}(4 x-1)^{2}$
Roots of this equation are the values for which $ (4 x-1)^{2}=0 $
Therefore,
$ (4 x-1)=0 \text { or }(4 x-1)=0 $
i.e., $ x=\frac{1}{4} r x=\frac{1}{4} $

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now

(v) $ 100 x^{2}-20 x+1=0 $

Answer

$ 100 x^{2}-20 x+1 $
$=100 x^{2}-10 x-10 x+1$
$=10 x(10 x-1)-1(10 x-1)$
$=(10 x-1)^{2}$
Roots of this equation are the values for which $ (10 x-1)^{2}=0 $
Therefore,
$ (10 \mathrm{x}-1)=0 $ or $ (10 \mathrm{x}-1)=0 $
i.e. $ x=\frac{1}{10} $ or $ x=\frac{1}{10} $

(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, andthe product of the number of marbles they now have is 124. We would like to findout how many marbles they had to start with.

Answer

(i) Let the number of John's marbles be x.
Therefore, number of Jivanti's marble $ =45-\mathrm{x} $
After losing $5$ marbles,
Number of John's marbles $ =\mathrm{x}-5 $
Number of Jivanti's marbles $ =45-\mathrm{x}-5=40-\mathrm{x} $
Given that the product of their marbles is $124$.
$ \therefore(\mathrm{x}-5)(40-\mathrm{x})=124$
$\Rightarrow \mathrm{x}^{2}-45 \mathrm{x}+324=0$
Now, to factorize this equation, we need to take numbers such that their product is $324$ and sum is $45$
$ \Rightarrow \mathrm{x}^{2}-36 \mathrm{x}-9 \mathrm{x}+324=0$
$\Rightarrow \mathrm{x}(\mathrm{x}-36)-9(\mathrm{x}-36)=0$
$\Rightarrow(\mathrm{x}-36)(\mathrm{x}-9)=0$
Either $ \mathrm{x}-36=0 $ or $ \mathrm{x}-9=0 $
i.e., $ x=36 $ or $ x=9 $
If the number of John's marbles $ =36 $,
Then, number of Jivanti's marbles $ =45-36=9 $
If number of John's marbles $ =9 $,
Then, number of Jivanti's marbles $ =45-9=36 $

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now

$Mathninja.in$

(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toysproduced in a day. On a particular day, the total cost of production was` 750. We would like to find out the number of toys produced on that day.

Answer

(ii) Let the number of toys produced be x.
$ \therefore $ Cost of production of each toy $ =\mathrm{Rs}(55-\mathrm{x}) $
It is given that, total production of the toys $ = $ Rs 750 \[\therefore \mathrm{x}(55-\mathrm{x})=750 \\ \Rightarrow \mathrm{x}^{2}-55 \mathrm{x}+750=0 \] Now to factorize this equation we have to find two numbers such that their product is 750 and sum is 55 \[\Rightarrow x^{2}-25 x-30 x+750=0 \\ \Rightarrow x(x-25)-30(x-25)=0 \\ \Rightarrow(x-25)(x-30)=0\]
Either $ \mathrm{x}-25=0 $ or $ \mathrm{x}-30=0 $
i.e., $ x=25 $ or $ x=30 $
Hence, the number of toys will be either 25 or 30 .

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now

3. Find two numbers whose sum is 27 and product is 182 .

Answer

Let the first number be x and the second number is $ 27-\mathrm{x} $.
[As the sum of both the numbers is 27]
Therefore, their product $ =\mathrm{x}(27-\mathrm{x}) $
It is given that the product of these numbers is 182 .
$ x(27-x)=182$
$-x^{2}+27 x-182=0$
Changing the signs on both sides we get, $ \mathrm{x}^{2}-27 \mathrm{x}+182=0 $
Factorizing we get, 13 and 14 are the numbers whose sum is 27 and product is 182
$ x^{2}-13 x-14 x+182=0$
$=x(x-13)-14(x-13)=0$
$ =(x-13)(x-14)=0 $
Either $ \mathrm{x}-13=0 $ or $ \mathrm{x}-14=0 $
i.e., $ x=13 $ or $ x=14 $
If first number $ =13 $, then
Other number $ =27-13=14 $
If first number $ =14 $, then
Other number $ =27-14=13 $
Therefore, the numbers are 13 and 14.

4. Find two consecutive positive integers, sum of whose squares is 365 .

Answer

To Find: Consecutive integers sum of whose square is 365. Consecutive integers mean that the difference between the integers is of 1 Let the consecutive positive integers be $ x $ and $ x+1 $.
Given that $ \mathrm{x}^{2}+(\mathrm{x}+1)^{2}=365 $
$ \Rightarrow x^{2}+x^{2}+1+2 x=365$
$\Rightarrow 2 x^{2}+2 x-364=0$
$\Rightarrow x^{2}+x-182=0$
Now to factorize the above quadratic equation, we need to
chose numbers such that their product is 182 and difference is 1.
$ \Rightarrow \mathrm{x}^{2}+14 \mathrm{x}-13 \mathrm{x}-182=0$
$\Rightarrow \mathrm{x}(\mathrm{x}+14)-13(\mathrm{x}+14)=0$
$(\mathrm{x}+14)(\mathrm{x}-13)=0$
Either $ x+14=0 $ or $ x-13=0 $, i.e., $ x=-14 $ or $ x=13 $
Since the question ask for positive integers, $ x $ can only be 13 .
$ \therefore x+1=13+1=14 $
Therefore, two consecutive positive integers will be 13 and 14 .

5. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm , find the other two sides.

Answer

Consider a right angle $ \triangle \mathrm{ABC} $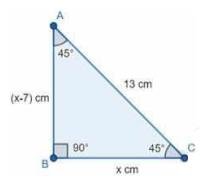

Let the base of the $ \Delta $ be $ x $
$ \Rightarrow $ Altitude $ =\mathrm{x}-7 $
In the right-angled triangle
According to the Pythagoras theorem
$ (\text { Hypotenuse })^{2}=(\text { base })^{2}+(\text { altitude })^{2} $
$ \Rightarrow 13^{2}=x^{2}+(x-7)^{2}$
$\Rightarrow 169-x^{2}-x^{2}-49+14 x=0$
$\Rightarrow 2 x^{2}-14 x-120=0$
$\Rightarrow x^{2}-7 x-60=0$
$\Rightarrow x^{2}-12 x+5 x-60=0$
$ \Rightarrow \mathrm{x}(\mathrm{x}-12)+5(\mathrm{x}-12)=0$
$\Rightarrow(\mathrm{x}+5)(\mathrm{x}-12)=0$
$\Rightarrow \mathrm{x}=-5 \text { or } 12$
But base cannot be negative, so $ x=12 \mathrm{~cm} $
$ \Rightarrow \text { altitude }=12-7=5 \mathrm{~cm} $
Hence 5 cm and 12 cm are the two sides of the given triangle.

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now

6. A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs 90, find the number of articles produced and cost of each article.

Answer

To find: Number of articles produced and cost of each article.
Let the number of articles produced be $ x $.
Therefore, cost of production of each article $ = $ Rs $ (2 x+3) $
The total cost of production $ = $ Total quantity produced x cost of one article.
It is given that the total cost of production is Rs 90.
$\therefore \mathrm{x}(2 \mathrm{x}+3)=90$
$\Rightarrow 2 \mathrm{x}^{2}+3 \mathrm{x}=90$
$\Rightarrow 2 \mathrm{x}^{2}+3 \mathrm{x}-90=0$
$\Rightarrow 2 \mathrm{x}^{2}+15 \mathrm{x}-12 \mathrm{x}-90=0$
$\Rightarrow \mathrm{x}(2 \mathrm{x}+15)-6(2 \mathrm{x}+15)=0$
$\Rightarrow(2 \mathrm{x}+15)(\mathrm{x}-6)=0$
Either $ 2 x+15=0 $ or $ x-6=0 $,
i.e., $ x=\frac{-15}{2} $ or $ x=6 $
As the number of articles produced can only be a positive
integer, Therefore, $ x $ can only be 6 .
Hence, the number of articles produced $ =6 $
Cost of each article $ =2 \times 6+3 $
$ =12+3=\operatorname{Rs} 15 \text {. } $

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now

CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)

Download the Math Ninja App Now