NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Explore the NCERT Solutions for Class 10 Maths Chapter 6: Triangle (English Medium), with detailed explanations for Exercise 6.5. This resource is designed to simplify complex Triangle, helping Class 10 Maths students grasp the subject effortlessly. For any queries regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangle Ex 6.5, feel free to leave a comment, and we’ll respond as soon as possible. || Class 10 Maths Chapter 6 Triangle Ex 6.5 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle (English Medium)

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5
Exercise - 6.5

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

1. Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.

(i) $ 7 \mathrm{~cm}, 24 \mathrm{~cm}, 25 \mathrm{~cm} $

Answer

Given: sides of the triangle are $ 7 \mathrm{~cm}, 24 \mathrm{~cm} $, and 25 cm
Squaring the lengths of these sides, we get: 49,576 , and 625.
$ 49+576=625 $
Or, $ 7^{2}+24^{2}=25^{2} $
The sides of the given triangle satisfy Pythagoras theorem Hence, it is a right triangle
We know that the longest side of a right triangle is the hypotenuse
Therefore, the length of the hypotenuse of this triangle is 25 cm

(ii) $ 3 \mathrm{~cm}, 8 \mathrm{~cm}, 6 \mathrm{~cm} $

Answer

It is given that the sides of the triangle are $ 3 \mathrm{~cm}, 8 \mathrm{~cm} $, and 6 cm
Squaring the lengths of these sides, we will obtain 9, 64, and 36
However, $ 9+36 \neq 64 $
Or, $ 32+62 \neq 82 $
Clearly, the sum of the squares of the lengths of two sides is not equal to the square of the length of the third side
Therefore, the given triangle is not satisfying Pythagoras theorem
Hence, it is not a right triangle

(iii) $ 50 \mathrm{~cm}, 80 \mathrm{~cm}, 100 \mathrm{~cm} $

Answer

Given that sides are $ 50 \mathrm{~cm}, 80 \mathrm{~cm} $, and 100 cm .
Squaring the lengths of these sides, we will obtain 2500, 6400, and 10000.
And, $ 2500+6400 \neq 10000 $
Or, $ 502+802 \neq 1002 $
Now, the sum of the squares of the lengths of two sides is not equal to the square of the length of the third side
Therefore, the given triangle is not satisfying Pythagoras theorem
Hence, it is not a right triangle

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

(iv) $ 13 \mathrm{~cm}, 12 \mathrm{~cm}, 5 \mathrm{~cm} $

Answer

Given: Sides are $ 13 \mathrm{~cm}, 12 \mathrm{~cm} $, and 5 cm
Squaring the lengths of these sides, we get 169, 144, and 25.
Clearly, $ 144+25=169 $
Or, $ 12^{2}+5^{2}=13^{2} $
The sides of the given triangle are satisfying Pythagoras theorem
Therefore, it is a right triangle
We know that the longest side of a right triangle is the hypotenuse
Therefore, the length of the hypotenuse of this triangle is 13 cm.

2. $ P Q R $ is a triangle right angled at $ P $ and $ M $ is a point on $ Q R $ such that $ \mathrm{PM} \perp \mathrm{QR} $. Show that $ \mathrm{PM}^{2}=\mathrm{QM} \times \mathrm{MR} $.

Answer

$ \Rightarrow $ Let $ \angle \mathrm{MPR}=\mathrm{x} $
$ \Rightarrow $ In $ \triangle \mathrm{MPR}, \angle \mathrm{MRP}=180-90-\mathrm{x} $
$ \Rightarrow \angle M R P=90-x $
Similarly in $ \triangle \mathrm{MPQ} $,
$ \angle M P Q=90-\angle M P R=90-x $
$ \Rightarrow \angle \mathrm{MQP}=180-90-(90-\mathrm{x}) $
$ \Rightarrow \angle \mathrm{MQP}=\mathrm{x} $
In $ \triangle \mathrm{QMP} $ and $ \triangle \mathrm{PMR} $
$ \Rightarrow \angle \mathrm{MPQ}=\angle \mathrm{MRP}$
$\Rightarrow \angle \mathrm{PMQ}=\angle \mathrm{RMP}$
$\Rightarrow \angle \mathrm{MQP}=\angle \mathrm{MPR}$
$\Rightarrow \triangle \mathrm{QMP} \sim \triangle \mathrm{PMR}$
$\Rightarrow \frac{Q M}{P M}=\frac{M P}{M R}$
$\Rightarrow \mathrm{PM}^{2}=\mathrm{MR} \times \mathrm{QM} $
Hence proved.

Q. 3 In Fig. 6.53, ABD is a triangle right angled at A and $ \mathrm{AC} \perp \mathrm{BD} $.

(i) $ \mathrm{AB}^{2}=\mathrm{BC} \cdot \mathrm{BD} $

Answer

In $ \triangle \mathrm{ADB} $ and $ \triangle \mathrm{CAB} $, we have
$ \angle \mathrm{DAB}=\angle \mathrm{ACB}\left(\right. $ Each of $ \left.90^{\circ}\right) $
$ \angle \mathrm{ABD}=\angle \mathrm{CBA} $ (Common angle)
Therefore,
$ \triangle \mathrm{ADB} \sim \triangle \mathrm{CAB} $ (AA similarity)
$ \frac{A B}{C B}=\frac{B D}{A B} $
$ \mathrm{AB}^{2}=\mathrm{CB} \times \mathrm{BD} $

(ii) $ \mathrm{AC}^{2}=\mathrm{BC} $. DC

Answer

Let $ \angle \mathrm{CAB}=\mathrm{x} $
In $ \triangle \mathrm{CBA} $,
$ \angle \mathrm{CBA}+\angle \mathrm{CAB}+\angle \mathrm{ACB}=180^{\circ} $
As, $ \angle \mathrm{ACB}=90^{\circ} $, we have
$ \angle \mathrm{CBA}=180^{\circ}-90^{\circ}-\mathrm{x} $
$ \angle \mathrm{CBA}=90^{\circ}-\mathrm{x} $
Similarly, in $ \triangle \mathrm{CAD} $
$ \angle \mathrm{CAD}=90^{\circ}-\angle \mathrm{CBA} $
$ =90^{\circ}-\mathrm{x} $
$ \angle \mathrm{CDA}=180^{\circ}-90^{\circ}-\left(90^{\circ}-\mathrm{x}\right) $
$ \angle \mathrm{CDA}=\mathrm{x} $
In triangle $ C B A $ and $ C A D $, we have
$ \angle \mathrm{CBA}=\angle \mathrm{CAD} $
$ \angle \mathrm{CAB}=\angle \mathrm{CDA} $
$ \angle \mathrm{ACB}=\angle \mathrm{DCA}\left(\right. $ Each $ \left.90^{\circ}\right) $
Therefore,
$ \triangle \mathrm{CBA}^{\sim} \triangle \mathrm{CAD} $ (By AAA similarity)
$ \frac{A C}{D C}=\frac{B C}{A C} $
$ \mathrm{AC}^{2}=\mathrm{DC} \times \mathrm{BC} $

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

(iii) $ \mathrm{AD}^{2}=\mathrm{BD} \cdot \mathrm{CD} $

Answer

In $ \triangle \mathrm{DCA} $ and $ \triangle \mathrm{DAB} $, we have
$ \angle \mathrm{DCA}=\angle \mathrm{DAB}\left(\right. $Each $ \left.90^{\circ}\right) $
$ \angle \mathrm{CDA}=\angle \mathrm{ADB} $ (Common angle)
Therefore,
$ \triangle \mathrm{DCA} \sim \triangle \mathrm{DAB} $ (By AA similarity)
$ \frac{D C}{D A}=\frac{D A}{B D}$
$\mathrm{AD}^{2}=\mathrm{BD} \times \mathrm{CD} $

4. ABC is an isosceles triangle right angled at $ C $. Prove that $ A B^{2} $ $ =2 \mathrm{AC}^{2} $.

Answer

To Prove: $ 2 \mathrm{AC}^{2}=\mathrm{AB}^{2} $
Given: $ \triangle \mathrm{ABC} $ is an isosceles triangle
Proof:
$ \mathrm{AC}=\mathrm{CB} $ (Two sides of an isosceles triangle are equal, as the side opposite to right angle is largest, rest of the two sides are equal)
Pythagoras Theorem: It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Using Pythagoras theorem in $ \triangle \mathrm{ABC} $ (i.e., right-angled at point C), we get
$ \mathrm{AC}^{2}+\mathrm{CB}^{2}=\mathrm{AB}^{2}$
$\mathrm{AC}^{2}+\mathrm{AC}^{2}=\mathrm{AB}^{2} \quad(\mathrm{AC}=\mathrm{CB})$
$\mathrm{So},$ $2 \mathrm{AC}^{2}=\mathrm{AB}^{2}$
Hence, Proved.

5. ABC is an isosceles triangle with $ \mathrm{AC}=\mathrm{BC} $. If $ \mathrm{AB}^{2}= $ $ 2 \mathrm{AC}^{2} $, prove that ABC is a right triangle.

Answer

To Prove: ABC is a right angled triangle Given: $ \mathrm{AB}^{2}=2 \mathrm{AC}^{2} $
Now $ 2 \mathrm{~AC}^{2} $ can be split into two parts
$ \mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{AC}^{2} $
in an isosceles triangle ABC two sides are equal, and it is given that $ \mathrm{AC}=\mathrm{BC} $. So,
$ \mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{BC}^{2}(\mathrm{As}, \mathrm{AC}=\mathrm{BC}) $
Now According to pythagoras theorem, in a right angled triangle, square of one side equals to the sum of squares of other two sides And clearly above equation satisfies it. Thus, the equation satisfies pythagoras theorem and the triangle should be right angled for that. Therefore, the given triangle is a right-angled triangle.
Hence, Proved.

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

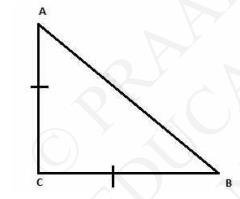
6. ABC is an equilateral triangle of side 2a. Find each of its altitudes

Answer

Let AD be the altitude of the given equilateral triangle, $ \triangle \mathrm{ABC} $
We know that altitude bisects the opposite side
$ \mathrm{BD}=\mathrm{DC}=\mathrm{a} $

In triangle ADB,
$ \angle \mathrm{ADB}=90^{\circ} $
Using Pythagoras theorem, we get
$ \mathrm{AD}^{2}+\mathrm{DB}^{2}=\mathrm{AB}^{2}$
$\mathrm{AD}^{2}+\mathrm{a}^{2}=(2 \mathrm{a})^{2}$
$\mathrm{AD}^{2}+\mathrm{a}^{2}=4 \mathrm{a}^{2}$
$\mathrm{AD}^{2}=3 \mathrm{a}^{2}$
$\mathrm{AD}=\mathrm{a} \sqrt{3} $
In an equilateral triangle, all the altitudes are equal in length.
Hence, the length of each altitude will be $ \sqrt{3} a $.

7. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

Answer

In Rhombus ABCD,
$ \mathrm{AB}, \mathrm{BC}, \mathrm{CD} $ and AD are the sides of the rhombus. BD and AC are the diagonals.
To prove: $ \mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}+\mathrm{AD}^{2}=\mathrm{AC}^{2}+\mathrm{BD}^{2} $
Proof:
The figure is shown below:

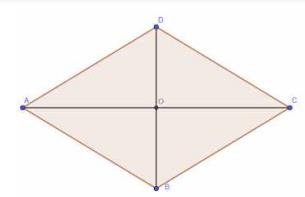
In $ \triangle \mathrm{AOB}, \triangle \mathrm{BOC}, \triangle \mathrm{COD}, \triangle \mathrm{AOD} $,
Applying Pythagoras theorem, we obtain
$ \mathrm{AB}^{2}=\mathrm{AO}^{2}+\mathrm{OB}^{2} \quad\ldots \text{(i)}$
$\mathrm{BC}^{2}=\mathrm{BO}^{2}+\mathrm{OC}^{2} \quad\ldots \text{(ii)}$
$\mathrm{CD}^{2}=\mathrm{CO}^{2}+\mathrm{OD}^{2} \quad\ldots \text{(iii)}$
$\mathrm{AD}^{2}=\mathrm{AO}^{2}+\mathrm{OD}^{2} \quad\ldots \text{(iv)}$
Now after adding all equations, we get,
$ \mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}+\mathrm{AD}^{2}=2\left(\mathrm{AO}^{2}+\mathrm{OB}^{2}+\mathrm{OC}^{2}+\mathrm{OD}^{2}\right) $
Diagonals of a rhombus bisect each other,
Thus $ \mathrm{AO}=\frac{ \mathrm{AC} }{ 2 }, \mathrm{OB}=\frac{ \mathrm{BD} }{ 2 }, \mathrm{OC}=\frac{ \mathrm{AC} }{ 2 } $, and $ \mathrm{OD}=\frac{ \mathrm{BD} }{ 2 } $
$ A B^{2}+B C^{2}+C D^{2}+A D^{2}=2$$\left[\left(\frac{A C}{2}\right)^{2}+\left(\frac{B D}{2}\right)^{2}+\left(\frac{A C}{2}\right)^{2}+\left(\frac{B D}{2}\right)^{2}\right]$
$=4\left[\frac{A C^{2}}{4}+\frac{B D^{2}}{4}\right]$
$=(\mathrm{AC})^{2}+(\mathrm{BD})^{2} $
Hence Sum of squares of sides of a rhombus equals to sum of squares of diagonals of rhombus.

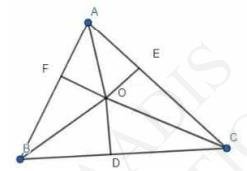
(i) In Fig. 6.54, O is a point in the interior of a triangle $ \mathrm{ABC}, \mathrm{OD} \perp $ $ \mathrm{BC}, \mathrm{OE} \perp \mathrm{AC} $ and $ \mathrm{OF} \perp \mathrm{AB} $. Show that

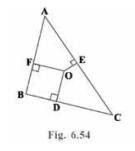
$ \mathrm{OA}^{2}+\mathrm{OB}^{2}+\mathrm{OC}^{2}-\mathrm{OD}^{2}-\mathrm{OE}^{2}-\mathrm{OF}^{2}=\mathrm{AF}^{2}+\mathrm{BD}^{2}+\mathrm{CE}^{2} $

Answer

To Prove
$ \mathrm{OA}^{2}+\mathrm{OB}^{2}+\mathrm{OC}^{2}-\mathrm{OD}^{2}-\mathrm{OE}^{2}-\mathrm{OF}^{2}=\mathrm{AF}^{2}+\mathrm{BD}^{2}+\mathrm{EC}^{2} $
Given: $ \mathrm{OD}, \mathrm{OE} $ and OF are perpendiculars on sides $ \mathrm{BC}, \mathrm{AC} $ and AB respectively
Construction : Join OA, OB and OC
Now according to pythagoras theorem, In a right angled triangle, (hypotenuse)$ ^{2}=(\text { altitude})^{2}+(\text { base})^{2} $
Applying Pythagoras theorem in $ \triangle \mathrm{AOF} $, we obtain
$ \mathrm{OA}^{2}=\mathrm{OF}^{2}+\mathrm{AF}^{2} \quad\ldots \text{(i)}$
Similarly, in $ \triangle \mathrm{BOD} $,
$ \mathrm{OB}^{2}=\mathrm{OD}^{2}+\mathrm{BD}^{2} \quad\ldots \text{(ii)}$
Similarly, in $ \triangle \mathrm{COE} $,
$ \mathrm{OC}^{2}=\mathrm{OE}^{2}+\mathrm{EC}^{2} \quad\ldots \text{(iii)}$
Adding these equations, we get
$ \mathrm{OA}^{2}+\mathrm{OB}^{2}+\mathrm{OC}^{2}=\mathrm{OF}^{2}+\mathrm{AF}^{2}+\mathrm{OD}^{2}+\mathrm{BD}^{2}+\mathrm{OE}^{2}+\mathrm{EC}^{2} $
Rearranging the equations we get,
$ \mathrm{OA}^{2}+\mathrm{OB}^{2}+\mathrm{OC}^{2}-\mathrm{OD}^{2}-\mathrm{OE}^{2}-\mathrm{OF}^{2}=\mathrm{AF}^{2}+\mathrm{BD}^{2}+\mathrm{EC}^{2} $
Hence, Proved

(ii) In Fig. 6.54, O is a point in the interior of a triangle $ \mathrm{ABC}, \mathrm{OD} \perp $ $ \mathrm{BC}, \mathrm{OE} \perp \mathrm{AC} $ and $ \mathrm{OF} \perp \mathrm{AB} $. Show that

$ \mathrm{AF}^{2}+\mathrm{BD}^{2}+\mathrm{CE}^{2}=\mathrm{AE}^{2}+\mathrm{CD}^{2}+\mathrm{BF}^{2} $

Answer

To Prove: $ \mathrm{AF}^{2}+\mathrm{BD}^{2}+\mathrm{EC}^{2}=\mathrm{AE}^{2}+\mathrm{CD}^{2}+\mathrm{BF}^{2} $
From the above given result from (i),
$ \mathrm{AF}^{2}+\mathrm{BD}^{2}+\mathrm{EC}^{2}$
$=\left(\mathrm{AO}^{2}-\mathrm{OE}^{2}\right)+\left(\mathrm{OC}^{2}-\mathrm{OD}^{2}\right)+\left(\mathrm{OB}^{2}-\mathrm{OF}^{2}\right) $
and from eq(i), (ii) and (iii)
$ \mathrm{AO}^{2}-\mathrm{OE}^{2}=\mathrm{AE}^{2}, \mathrm{OC}^{2}-\mathrm{OD}^{2}=\mathrm{CD}^{2}, \mathrm{OB}^{2}-\mathrm{OF}^{2}-\mathrm{BF}^{2} $
Putting these values in above equation we get,
$ \mathrm{AF}^{2}+\mathrm{BD}^{2}+\mathrm{EC}^{2}=\mathrm{AE}^{2}+\mathrm{CD}^{2}+\mathrm{BF}^{2} $
Hence, Proved

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

$Mathninja.in$

9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall

Answer

Let OA be the wall and AB be the ladder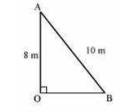

By Pythagoras theorem, $ \mathrm{AB}^{2}=\mathrm{OA}^{2}+\mathrm{BO}^{2} $
$ (10)^{2}=(8)^{2}+\mathrm{OB}^{2}$
$100=64+\mathrm{OB}^{2}$
$\mathrm{OB}^{2}=36$
$\mathrm{OB}=6 \mathrm{~cm} $
Therefore, the distance of the foot of the ladder from the base of the wall is 6 m .

10. A wire attached to a vertical pole of height 18 m is 24 m long and has a stack attached to the other end. How far from the base of the pole should the stack be driven so that the wire will be taut?

Answer

To find: OA
Let OB be the pole and AB be the wire
By Pythagoras theorem,
Pythagoras Theorem: the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.

$ \mathrm{AB}^{2}=\mathrm{OB}^{2}+\mathrm{OA}^{2} $
$ (24)^{2}=(18)^{2}+\mathrm{OA}^{2} $
$ \mathrm{OA}^{2}=(576-324) $
$ \mathrm{OA}^{2}=252 $
$ \mathrm{OA}=6 \sqrt{7 } \mathrm{~m} $

11. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after $ 1 \frac{1}{2} $ hours?

Answer

we know, Distance $ = $ speed $ \times $ time Distance traveled by the plane flying towards north in $ 1 \frac{1}{2} h r s=1,000 \times 1 \frac{1}{2} $ $ =1,500 \mathrm{~km} $
Similarly, distance traveled by the plane flying towards west in $1 \frac{1}{2} h r s=1,200 \times 1 \frac{1}{2}$
$=1,800 \mathrm{~km} $
Let these distances be represented by OA and OB respectively.
Pythagoras Theorem: It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Applying Pythagoras theorem,
$\mathrm{AB}^{2}=\mathrm{OA}^{2}+\mathrm{OB}^{2}$
$A B=\sqrt{O A^{2}+O B^{2}}$
$A B=\sqrt{(1500)^{2}+(1800)^{2}}$
$A B=\sqrt{2250000+3240000}$
$A B=\sqrt{5490000}$
$A B=300 \sqrt{61} $
Distances between planes is $ 300 \sqrt{6} 1 \mathrm{~km} $.

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

12. Two poles of heights 6 m and 11 m stand on aplane ground. If the distance between the feet of the poles is 12 m , find the distance between their tops

Answer

Let CD and $ A B $ be the poles of height 11 m and 6 m Therefore, $ \mathrm{CP}=11-6=5 \mathrm{~m} $
From the figure, it can be observed that $ \mathrm{AP}=12 \mathrm{~m} $ Applying Pythagoras theorem for $ \triangle \mathrm{APC} $, we obtain

$ \mathrm{AP}^{2}+\mathrm{PC}^{2}=\mathrm{AC}^{2}$
$(12)^{2}+(5)^{2}=\mathrm{AC}^{2}$
$\mathrm{AC}^{2}=(144+25)$
$\mathrm{AC}^{2}=169$
$\mathrm{AC}=13 \mathrm{~m} $
Therefore, the distance between their tops is 13 m

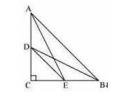
13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C . Prove that $ \mathrm{AE}^{2}+\mathrm{BD}^{2}=\mathrm{AB}^{2}+\mathrm{DE}^{2} $

Answer

Prove: $ \mathrm{AE}^{2}+\mathrm{BD}^{2}=\mathrm{AB}^{2}+\mathrm{DE}^{2} $
Given: D and E are midpoints of AD and CB and ABC is right angled at C
Applying Pythagoras theorem in $ \triangle \mathrm{ACE} $, we obtain

Pythagoras theorem: It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
$ \mathrm{AC}^{2}+\mathrm{CE}^{2}=\mathrm{AE}^{2} \quad\ldots \text{(i)}$
Applying Pythagoras theorem in triangle BCD , we get
$ \mathrm{BC}^{2}+\mathrm{CD}^{2}=\mathrm{BD}^{2} \quad\ldots \text{(ii)}$
Adding equations (i) and (ii), we get
$ \mathrm{AC}^{2}+\mathrm{CE}^{2}+\mathrm{BC}^{2}+\mathrm{CD}^{2}=\mathrm{AE}^{2}+\mathrm{BD}^{2} \quad\ldots \text{(iii)}$
Applying Pythagoras theorem in triangle CDE, we get
$ \mathrm{DE}^{2}=\mathrm{CD}^{2}+\mathrm{CE}^{2} $
Applying Pythagoras in triangle ABC , we get
$ \mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{CB}^{2} $
Putting these values in eqn(iii), we get
$ \mathrm{DE}^{2}+\mathrm{AB}^{2}=\mathrm{AE}^{2}+\mathrm{BD}^{2} $
Hence, Proved.

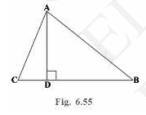
14. The perpendicular from $ A $ on side $ B C $ of a $ \triangle A B C $ intersects $ B C $ at D such that $ \mathrm{DB}=3 \mathrm{CD} $ (see Fig. 6.55). Prove that $ 2 \mathrm{AB}^{2}=2 \mathrm{AC}^{2}+ $ $ \mathrm{BC}^{2} $

Answer

We have two right angled triangles now $ \triangle \mathrm{ACD} $ and $ \triangle \mathrm{ABD} $
Applying Pythagoras theorem for $ \triangle \mathrm{ACD} $, we obtain
$ \mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{DC}^{2} $
$ \mathrm{AD}^{2}=\mathrm{AC}^{2}-\mathrm{DC}^{2}\quad\ldots \text{(i)}$
Applying Pythagoras theorem in $ \triangle \mathrm{ABD} $, we obtain
$ \mathrm{AB}^{2}=\mathrm{AD}^{2}+\mathrm{DB}^{2} $
$ \mathrm{AD}^{2}=\mathrm{AB}^{2}-\mathrm{DB}^{2} \quad\ldots \text{(ii)}$
Now we can see from equation $ i $ and equation ii that LHS is
same. Thus,
From (i) and (ii), we get
$ \mathrm{AC}^{2}-\mathrm{DC}^{2}=\mathrm{AB}^{2}-\mathrm{DB}^{2} \quad\ldots \text{(iii)}$
It is given that $ 3 \mathrm{DC}=\mathrm{DB} $
Therefore,
$ \mathrm{DC}+\mathrm{DB}=\mathrm{BC} $
$ \mathrm{DC}+3 \mathrm{DC}=\mathrm{BC} $
$ 4 \mathrm{DC}=\mathrm{BC} \quad\ldots \text{(iv)}$ and also, $ \mathrm{DC}=\frac{\mathrm{DB} }{ 3} $ putting this in eq (iii) $ \mathrm{DB}=\frac{3 B C}{4} $
So,
$ D C=\frac{B C}{4} $ and $ D B=\frac{3 B C}{4} $
Putting these values in (iii), we get
$ A C^{2}-\left(\frac{B C}{4}\right)^{2}=A B^{2}-\left(\frac{3 B C}{4}\right)^{2}$
$A C^{2}-B C \times \frac{B C}{16}=A B^{2}-\frac{9 \times B C \times B C}{16}$
$16 \mathrm{AC}^{2}-\mathrm{BC}^{2}=16 \mathrm{AB}^{2}-9 \mathrm{BC}^{2}$
$16 \mathrm{AB}^{2}-16 \mathrm{AC}^{2}=8 \mathrm{BC}^{2}$
$2 \mathrm{AB}^{2}=2 \mathrm{AC}^{2}+\mathrm{BC}^{2} $

15. In an equilateral triangle $ A B C, D $ is a point on side $ B C $ such that $ B D=\frac{1}{3} B C $ Prove that $ 9 \mathrm{AD}^{2}=7 \mathrm{AB}^{2} $

Answer

The figure is given below: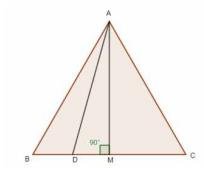

Given: $ \mathrm{B D}=\frac{ \mathrm{B C} }{ 3 } $
To Prove: $ 9 \mathrm{AD}^{2}=7 \mathrm{AB}^{2} $
Proof:
Let the side of the equilateral triangle be $ a $, and AM be the altitude of $ \triangle \mathrm{ABC} $
$ \mathrm{BM}=\mathrm{MC}=\frac{ \mathrm{BC} }{ 2 }=\frac{ \mathrm{a} }{ 2 }$ $\quad$ [Altitude of an equilateral triangle bisect the side]
And, then, in $ \triangle \mathrm{ABM} $, by pythagoras theorem we write, Pythagoras Theorem : Square of the Hypotenuse equals to the sum of the squares of other two sides.
$ \mathrm{AM}^{2}=\mathrm{AB}^{2}-\mathrm{BM}^{2}$
$\text {or } \mathrm{AM}^{2}=\mathrm{a}^{2}-\frac{ \mathrm{a}^{2} }{ 4 }$
$A M^{2}=\frac{4 a^{2}-a^{2}}{4}=\frac{3 a^{2}}{4}$
$A M=\frac{a \sqrt{3}}{2}$
$\mathrm{BD}=\frac{ \mathrm{a} }{ 3 }$ $\quad$ [$BC=a$]
$\mathrm{DM}=\mathrm{BM}-\mathrm{BD}$
$=\frac{ \mathrm{a} }{ 2 }-\frac{ \mathrm{a} }{ 3 }$
$=\frac{ \mathrm{a} }{ 6 } $
According to pythagoras theorem in a right angled triangle, $ (\text {hypotenuse})^{2}=(\text {altitude})^{2}+(\text {base})^{2} $
Applying Pythagoras theorem in $ \triangle \mathrm{ADM} $, we obtain $ \mathrm{AD}^{2}=\mathrm{AM}^{2}+\mathrm{DM}^{2}$
$A D^{2}=\left(\frac{a \sqrt{3}}{2}\right)^{2}+\left(\frac{a}{6}\right)^{2}$
$A D^{2}=\frac{3 a^{2}}{4}+\frac{a^{2}}{36}$
$A D^{2}=\frac{27 a^{2}+a^{2}}{36}$
$A D^{2}=\frac{28 a^{2}}{36} $
Now, $ \mathrm{a}=\mathrm{AB} $ or $ \mathrm{a}^{2}=\mathrm{AB}^{2} $
$ A D^{2}=\frac{28 A B^{2}}{36}$
$36 \mathrm{AD}^{2}=28 \mathrm{AB}^{2}$
$9 \mathrm{AD}^{2}=7 \mathrm{AB}^{2} $
Hence, Proved.

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

$Mathninja.in$

16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes

Answer

Let the side of the equilateral triangle be a, and AE be the altitude of $ \triangle \mathrm{ABC} $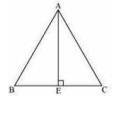

To Prove: $ 4 \times( $Square of altitude$ )=3 \times( $Square of one side$ ) $
Proof:
Altitude of equilateral triangle divides the side in two equal parts.
Therefore,
$ B E=E C=\frac{B C}{2}=\frac{a}{2} $
Pythagoras Theorem: It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Applying Pythagoras theorem in $ \triangle \mathrm{ABE} $, we obtain
$ \mathrm{AB}^{2}=\mathrm{AE}^{2}+\mathrm{BE}^{2}$
$a^{2}=A E^{2}+\frac{a^{2}}{4}$
$A E^{2}=a^{2}-\frac{a^{2}}{4}$
$A E^{2}=\frac{3 a^{2}}{4}$
$A E=\frac{\sqrt{3} a}{2}$
$4 \times A E^{2}=3 \times a^{2} $
$ 4 \times( $Square of altitude $ )=3 \times( $Square of one side$ ) $

17. Tick the correct answer and justify:
In $ \triangle \mathrm{ABC}, \mathrm{AB}=6 \sqrt{3} \mathrm{~cm}, \mathrm{AC}=12 \mathrm{~cm} $ and $ \mathrm{BC}=6 \mathrm{~cm} $, the angle B is:
A. $ 120^{\circ} $ B. $ 60^{\circ} $
C. $ 90^{\circ} $ D. $ 45^{\circ} $

Answer

Given that, $ \mathrm{AB}=6 \sqrt{3} \mathrm{~cm} $,
$ \mathrm{AC}=12 \mathrm{~cm} $,
And $ \mathrm{BC}=6 \mathrm{~cm} $
It can be observed that
$ \mathrm{AB}^{2}=108$
$\mathrm{AC}^{2}=144 $
And, $ \mathrm{BC}^{2}=36 $
$ \mathrm{AB}^{2}+\mathrm{BC}^{2}=\mathrm{AC}^{2} $
Pythagoras Theorem: It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
$ \triangle \mathrm{ABC} $, is satisfying Pythagoras theorem.
Therefore, the triangle is a right triangle, right-angled at B
$ \angle \mathrm{B}=90^{\circ} $
Hence, the correct answer is (C).

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now

NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5

Download the Math Ninja App Now