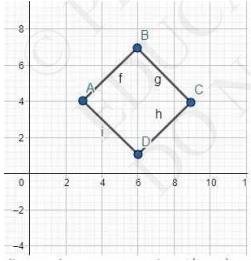
6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
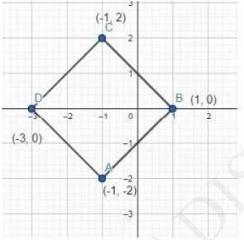
(i) \( (-1,-2),(1,0),(-1,2),(-3,0) \)
Answer
To Find: Type of quadrilateral formedLet the points \( (-1,-2),(1,0),(-1,2) \), and \( (-3,0) \) be representing the vertices \( A, B, C \),
and D of the given quadrilateral respectively
he distance formula is an algebraic expression used to determine the distance between two points with the coordinates \( \left(x_{1}, y_{1}\right) \) and \( \left(x_{2}, y_{2}\right) \).
\( D=\sqrt{ \left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \)\(\mathrm{AB}=\left[(-1-1)^{2}+(-2-0)^{2}\right]^{\frac{1}{2}}\)
\(=\sqrt{4+4}=\sqrt{8}\)
\(=2 \sqrt{ 2}\)
\(\mathrm{BC}=\sqrt{ \left[(1+1)^{2}+(0-2)^{2}\right]}\)
\(=\sqrt{4+4}=\sqrt{8}\)
\(=2 \sqrt{ 2}\)
\(\mathrm{AD}=\sqrt{ \left[(-1+3)^{2}+(-2-0)^{2}\right]}\)
\(=\sqrt{4+4}=\sqrt{8}\)
\(=2 \sqrt{ } 2\)
Diagonal \( A C=\sqrt{ \left[(-1+1)^{2}+(-2-2)^{2}\right] }\)
\(\sqrt{0+16}\)
\( =4 \)
Diagonal BD \( =\sqrt{ \left[(1+3)^{2}+(0-0)^{2}\right] }\)
\(\sqrt{16+0}\)
\(=4\)
It is clear that all sides of this quadrilateral are of the same length and the diagonals are of the same length. Therefore, the given points are the vertices of a square
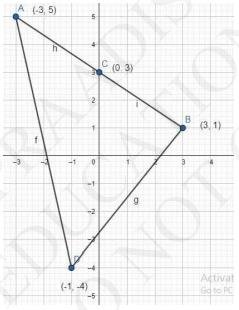
(ii) \( (-3,5),(3,1),(0,3),(-1,-4) \)
Answer
To Find: Type of quadrilateral formedLet the points \( (-3,5),(3,1),(0,3) \), and \( (-1,-4) \) be representing the vertices \( A, B, C \), and \( D \) of the given quadrilateral respectively.
The distance formula is an algebraic expression used to determine the distance between two points with the coordinates ( \( x_{1}, y_{1} \) ) and \( \left(x_{2}, y_{2}\right) \).
\(D=\sqrt{ \left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
\(A B=\sqrt{ \left[(-3-3)^{2}+(5-1)^{2}\right]}\)
\(\sqrt{36+16}=\sqrt{52}\)
\(=2 \sqrt{ 13}\)
\(\mathrm{BC}=\sqrt{ \left[(3-0)^{2}+(1-3)^{2}\right]}\)
\(=\sqrt{9+4}\)
\(=\sqrt{13}\)
\(\mathrm{CD}=\sqrt{ [(0+1)^2+(3+4)^2]}\)
\(=\sqrt{1+49}=\sqrt{50}\)
\(=5 \sqrt{ 2}\)
\(\mathrm{AD}=\sqrt{ \left[(-3+1)^{2}+(5+4)^{2}\right]}\)
\(=\sqrt{4+81}\)
\(=\sqrt{85}\)
We can observe that all sides of this quadrilateral are of different lengths.
Therefore, it can be said that it is only a general quadrilateral, and not specific such as square, rectangle, etc.
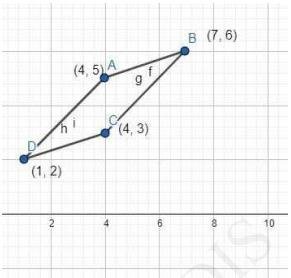
(iii) \( (4,5),(7,6),(4,3),(1,2) \)
Answer
To Find: Type of quadrilateral formedLet the points \( (4,5),(7,6),(4,3) \), and \( (1,2) \) be representing the vertices \( \mathrm{A}, \mathrm{B}, \mathrm{C} \), and D of the given quadrilateral respectively
The distance formula is an algebraic expression used to determine the distance between two points with the coordinates ( \( x_{1}, y_{1} \) ) and \( \left(x_{2}, y_{2}\right) \).
\(D=\sqrt{ \left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
\(\mathrm{AB}=\sqrt{\left[(4-7)^{2}+(5-6)^{2}\right] }\)
\(=\sqrt{9+1}\)
\(=\sqrt{10}\)
\(\mathrm{BC}=\sqrt{ \left[(7-4)^{2}+(6-3)^{2}\right]}\)
\(=\sqrt{9+9}\)
\(=\sqrt{18}\)
\(\mathrm{CD}=\sqrt{ \left[(4-1)^{2}+(3-2)^{2}\right]}\)
\(=\sqrt{9+1}\)
\(=\sqrt{10}\)
\(\mathrm{AD}=\sqrt{\left[(4-1)^{2}+(5-2)^{2}\right] }\)
\(=\sqrt{9+9}\)
\(=\sqrt{18}\)
\(\text { Diagonal }AC =\sqrt{\left[(4-4)^{2}+(5-3)^{2}\right]}\)
\(=\sqrt{0+4}\)
\(=2\)
\(\text { Diagonal }BD =\sqrt{ \left[(7-1)^{2}+(6-2)^{2}\right]}\)
\(=\sqrt{36+16}\)
\(=\sqrt{52}\)
\(=2 \sqrt{ 13}\)
We can observe that opposite sides of this quadrilateral are of the same length.
However, the diagonals are of different lengths. Therefore, the given points are the vertices of a parallelogram.
NCERT Math Solutions for Class 10 Maths Chapter 7 Coordinate Geometry(English Medium) || CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Download the Math Ninja App Now
7. Find the point on the \(x \)-axis which is equidistant from \( (2,-5) \) and \( (-2,9) \).
Answer
We have to find a point on \( x \)-axis.Hence, its \( y \)-coordinate will be 0
Let the point on \( x \)-axis be ( \( x, 0 \) )
By distance formula, Distance between two points \( \mathrm{A}\left(x_{1}, y_{1}\right) \) and \( \mathrm{B}\left(x_{2}\right. \), \( y_{2} \) ) is
\(A B=\sqrt{ \left(\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}\right)}\)
Distance between \( (x, 0) \) and \( (2,-5)=\sqrt{ \left[(x-2)^{2}+(0+5)^{2}\right] }\)
\(=\sqrt{ \left[(x-2)^{2}+(5)^{2}\right]}\)
Distance between \( (x, 0) \) and \( (-2,9)=\sqrt{ \left[(x+2)^{2}+(0+9)^{2}\right] }\)
\(=\sqrt{ \left[(x+2)^{2}+(9)^{2}\right]}\)
By the given condition, these distances are equal in measure
\(\sqrt{ \left[(x-2)^{2}+(5)^{2}\right]}=\sqrt{ \left[(x+2)^{2}+(9)^{2}\right]}\)
Squaring both sides we get,
\((x-2)^{2}+25=(x+2)^{2}+81\)
\(\Rightarrow x^{2}+4-4 x+25=x^{2}+4+4 x+81\)
\(\Rightarrow\left(x^{2}-x^{2}\right)-4 x-4 x=81-25\)
\(\Rightarrow-8 x=56\)
\(\Rightarrow 8 x=-56\)
\(\Rightarrow x=-7\)
Therefore, the point is \( (-7,0) \)
8. Find the values of \( y \) for which the distance between the points \( \mathrm{P}(2,-3) \) and \( \mathrm{Q}(10, \mathrm{y}) \) is 10 units.
Answer
Given: Distance between \( (2,-3) \) and \( (10, y) \) is 10To find: \( y \)
By distance formula, Distance between two points \( \mathrm{A}\left(x_{1}, y_{1}\right) \) and \( \mathrm{B}\left(x_{2}\right. \), \( y_{2} \) ) is
\(\mathrm{AB}=\sqrt{ \left(\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}\right)}\)
Therefore,
\(\sqrt{ \left[(2-10)^{2}+(-3-y)^{2}\right]}=10\)
\(\sqrt{ \left[(-8)^{2}+(3+y)^{2}\right]}=10\)
Squaring both sides to remove the square root,
\(\Rightarrow 64+(y+3)^{2}=100\)
\(\Rightarrow(y+3)^{2}=100-64\)
\(\Rightarrow(y+3)^{2}=36\)
\(\Rightarrow y+3= \pm 6\)
\( \Rightarrow(y+3) \) will give two values 6 and -6 as answer because both the values when squared will give 36 as answer.)
\(y+3=6 \text { or } y+3=-6\)
Therefore, \( y=3 \) or \(-9\)
9. If \( \mathrm{Q}(0,1) \) is equidistant from \( P(5,-3) \) and \( R(x, 6) \), find the values of \( x \). Also find the distances \( Q R \) and \( P R \).
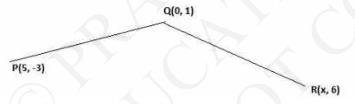

Answer
We know, By distance formula distance between two coordinates \( \mathrm{A}\left(x_{1}, y_{1}\right) \) and \( \mathrm{B}\left(x_{2}, y_{2}\right) \) is\(\mathrm{AB}=\sqrt{\left[\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}\right] }\)
Now, as \( \mathrm{PQ}=\mathrm{QR} \)
\(\sqrt{\left[(5-0)^{2}+(-3-1)^{2}\right] }=\sqrt{\left[(0-x)^{2}+(1-6)^{2}\right] }\)
\(\sqrt{25+16}= \sqrt{x^{2}+25}\)
Squaring both sides,
\(41=x^{2}+25\)
\(x^{2}=16\)
\(x= \pm 4\)
Hence, point \( R \) is \( (4,6) \) or \( (-4,6) \).
When point \( R \) is \( (4,6) \)
\(\operatorname{PR}=\left[(5-4)^{2}+(-3-6)^{2}\right]^{\frac{1}{2}}\)
\(=\sqrt{1+81}\)
\(=\sqrt{82}\)
\(\mathrm{QR}=\left[(0-4)^{2}+(1-6)^{2}\right]^{\frac{1}{2}}\)
\(=\sqrt{16+25}\)
\(=\sqrt{41}\)
When point R is \( (-4,6) \),
\(\mathrm{PR}=\left[(5+4)^{2}+(-3-6)^{2}\right]^{\frac{1}{2}}\)
\(\sqrt{81+81}\)
\(9 \sqrt{2}\)
\(\mathrm{QR}=\left[(0+4)^{2}+(1-6)^{2}\right]^{\frac{1}{2}}\)
\(\sqrt{16+25}\)
\(\sqrt{41}\)
10. Find a relation between \( x \) and \( y \) such that the point \( (x, y) \) is equidistant from the point \( (3,6) \) and \( (-3,4) \).
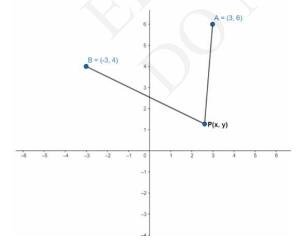

Answer
To Find: Relation between \( x \) and \( y \)Given: \( (x, y) \) is equidistant from \( (3,6) \) and \( (-3,4) \)
From the figure it can be seen that \( \operatorname{Point}(x, y) \)
is equidistant from \( (3, 6) \) and \( (-3,4) \)
This means that the distance of \( (x, y) \) from \( (3,6) \) will be equal to distance of \( (x, y) \) from \( (-3,4) \)
We know by distance formula that, distance between two points \( \mathrm{A}\left(x_{1}, y_{1}\right),
\mathrm{B}\left(x_{2}, y_{2}\right) \) is given by\(D=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Therefore,
\(\sqrt{ \left[(x-3)^{2}+(y-6)^{2}\right]}=\sqrt{ \left[(x+3)^{2}+(y-4)^{2}\right]}\)
Squaring both sides, we get
\((x-3)^{2}+(y-6)^{2}=(x+3)^{2}+(y-4)^{2}\)
\(x^{2}+9-6 x+y^{2}+36-12 y=x^{2}+9+6 x+y^{2}+16-8 y\)
\(36-16=6 x+6 x+12 y-8 y\)
\(20=12 x+4 y\)
\(3 x+y=5\)
\( 3 x+y-5=0 \) is the relation between \( x \) and \( y \).
NCERT Math Solutions for Class 10 Maths Chapter 7 Coordinate Geometry(English Medium) || CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Download the Math Ninja App NowCentral Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.3
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.4
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.5
Class 10 : CBSE Class 10 Maths Chapter 3: Pair of Linear Equations in Two Variables || CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.6
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3 || NCERT Solutions for Class 10 Maths Chapter 4: Quadratic Equations (English Medium)
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.1
Class 10 : NCERT Math Solutions for Class 10 Maths Chapter 6 Triangle(English Medium) || CBSE Class 10 Maths Chapter 6 Triangle Ex 6.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2