Ex 6.2 class 12 maths ncert solutions

Let \( x_{1} \) and \( x_{2} \) be any two numbers in \( R \).
Then, we have,
\(
x_{1} < x_{2}\)
\(\Rightarrow 3 x_{1} < 3x_{2}\)
\(\Rightarrow 3 x_{1}+17 < 3 x_{2}+17\)
\(\Rightarrow \mathrm{f}\left(x_{1}\right) < \mathrm{f}\left(x_{2}\right)
\)
Therefore, f is strictly increasing on R .

Let \( x_{1} \) and \( x_{2} \) be any two numbers in \( R \).
The, we have,
\(x_{1} < x_{2}\)
\(\Rightarrow 2 x_{1} < 2 x_{2}\)
\(\Rightarrow \mathrm{e}^{2 x_{1}} < \mathrm{e}^{2 x_{2}}\)
\(\Rightarrow \mathrm{f}\left(x_{1}\right) < \mathrm{f}\left(x_{2}\right)\)
Therefore, \( f \) is strictly increasing on \( R \)

(a) The function is \( f(x)=\sin x \)
Then, \( \mathrm{f}^{\prime}(x)=\cos x \)
Since for each \( x \in\left(0, \frac{\pi}{2}\right), \cos x > 0 \), we have \( f^{\prime}(x) > 0 \)
Therefore, \( \mathrm{f}^{\prime} \) is strictly increasing in \( \left(0, \frac{\pi}{2}\right) \).

The function is \( f(x)=\sin x \)
Then, \( f^{\prime}(x)=\cos x \)
Since for each \( x \in\left(\frac{\pi}{2}, \pi\right), \cos x < 0 \), we have \( \mathrm{f}^{\prime}(x) < 0 \)
Therefore, \( \mathrm{f}^{\prime} \) is strictly decreasing in \( \left(\frac{\pi}{2}, \pi\right) \).

The function is \( f(x)=\sin x \)
Then, \( \mathrm{f}^{\prime}(x)=\cos x \)
Since for each \( x \in\left(0, \frac{\pi}{2}\right), \cos x > 0 \), we have \( f^{\prime}(x) > 0 \)
Therefore, \( \mathrm{f}^{\prime} \) is strictly increasing in \( \left(0, \frac{\pi}{2}\right)\ldots(1) \)
Now, The function is \( f(x)=\sin x \)
Then, \( \mathrm{f}^{\prime}(x)=\cos x \)
Since, for each \( x \in\left(0, \frac{\pi}{2}\right), \cos x < 0 \), we have \( \mathrm{f}^{\prime}(x) < 0 \)
Therefore, \( \mathrm{f}^{\prime} \) is strictly decreasing in \( \left(\frac{\pi}{2}, \pi\right) \ldots(2)\)
From (1) and (2),
It is clear that f is neither increasing nor decreasing in \( (0, \pi) \).

It is given that function \( f(x)=2 x^{2}-3 x \)
\(
\Rightarrow \mathrm{f}^{\prime}(x)=4 x-3
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
x=\frac{3}{4}
\)
So, the points \( \frac{3}{4} \) divides the real line into two disjoint intervals, \( \left(-\infty, \frac{3}{4}\right) \) and \( \left(\frac{3}{4}, \infty\right) \)

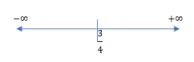
So, in interval \( \left(\frac{3}{4}, \infty\right), f^{\prime}(x)=4 x-3 > 0 \)
Therefore, the given function (f) is strictly increasing in interval \( \left(\frac{3}{4}, \infty\right) \).

It is given that function \( f(x)=2 x^{2}-3 x \)
\(\Rightarrow \mathrm{f}^{\prime}(x)=4x-3
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
x=\frac{3}{4}
\)
So, the points \( \frac{3}{4} \) divides the real line into two disjoint intervals, \( \left(-\infty, \frac{3}{4}\right) \) and \( \left(\frac{3}{4}, \infty\right) \).

So, in interval \( \left(-\infty, \frac{3}{4}\right) \quad f^{\prime}(x)=4 x-3 < 0 \)
Therefore, the given function ( f ) is strictly decreasing in interval \( \left(\frac{3}{4}, \infty\right) \).

It is given that function \( f(x)=2 x^{3}-3 x^{2}-36 x+7 \)
\(
\Rightarrow \mathrm{f}^{\prime}(x)=6 x^{2}-6 x+36\)
\(\Rightarrow \mathrm{f}^{\prime}(x)=6\left(x^{2}-x+6\right)\)
\(\Rightarrow \mathrm{f}^{\prime}(x)=6(x+2)(x-3)
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
\Rightarrow x=-2,3
\)
So, the points \( x=-2 \) and \( x=3 \) divides the real line into two disjoint intervals, \( (-\infty, 2),(-2,3) \) and \( (3, \infty) \)

So, in interval \( (-\infty, 2),(3, \infty) \)
\(
f^{\prime}(x)=6(x+2)(x-3) > 0
\)
Therefore, the given function (f) is strictly increasing in interval \( (-\infty, 2) \), \( (3, \infty) \).

It is given that function \( f(x)=2 x^{3}-3 x^{2}-36 x+7 \)
\(
\begin{array}{l}
\Rightarrow \mathrm{f}^{\prime}(x)=6 x^{2}-6 x+36 \\
\Rightarrow \mathrm{f}^{\prime}(x)=6\left(x^{2}-x+6\right) \\
\Rightarrow \mathrm{f}^{\prime}(x)=6(x+2)(x-3)
\end{array}
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
\Rightarrow x=-2,3
\)
So, the points \( x=-2 \) and \( x=3 \) divides the real line into two disjoint intervals, \( (-\infty, 2),(-2,3) \) and \( (3, \infty) \)

So, in interval \( (-2,3) \)
\(
f^{\prime}(x)=6(x+2)(x-3) < 0
\)
Therefore, the given function ( f ) is strictly decreasing in interval \( (-2,3) \).

It is given that function \( f(x)=x^{2}+2 x-5 \)
\(
f^{\prime}(x)=2 x+2
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
\Rightarrow x=-1
\)
So, the point \( x=-1 \) divides the real line into two disjoint intervals, \( (-\infty,- \) 1) and \( (1, \infty) \)
So, in interval \( (-\infty,-1) \)
\(
\mathrm{f}^{\prime}(x)=2 x+2 < 0
\)
Therefore, the given function (f) is strictly decreasing in interval \( (-\infty,-1) \).
And in interval \( (1, \infty) \)
\(
f^{\prime}(x)=2 x+2 > 0
\)
Therefore, the given function (f) is strictly increasing in interval \( (1, \infty) \). Thus, f is strictly increasing for \( x > -1 \).

It is given that function \( f(x)=10-6 x-2 x^{2} \)
\(
f^{\prime}(x)=-6-4 x
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
\Rightarrow x=\frac{-3}{2} .
\)
So, the point \( x=\frac{-3}{2} \) divides the real line into two disjoint intervals,
\(
\left(-\infty, \frac{-3}{2}\right) \text { and }\left(\frac{-3}{2}, \infty\right)
\)
So, in interval \( \left(-\infty, \frac{-3}{2}\right) \)
\(
x < \frac{-3}{2}\)
\(-4 x > 6-6-4 x > 0\)
\(f^{\prime}(x)=-6-4 x > 0
\)
Therefore, the given function (f) is strictly increasing in interval \( \left(-\infty, \frac{-3}{2}\right) \).
And in interval \( \left(\frac{-3}{2}, \infty\right) \)
\(
f^{\prime}(x)=-6-4 x < 0
\)
Therefore, the given function (f) is strictly decreasing in interval \( \left(\frac{-3}{2}, \infty\right) \).
Thus, \( f \) is strictly decreasing for \( x > \frac{-3}{2} \).

It is given that function \( f(x)=-2 x^{3}-9 x^{2}-12 x+1 \)
\(
\Rightarrow f^{\prime}(x)=-6 x^{2}-18 x+12\)
\(\Rightarrow f^{\prime}(x)=-6\left(x^{2}+3 x+6\right)\)
\(\Rightarrow f^{\prime}(x)=-6(x+1)(x+2)
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
\Rightarrow x=-1 \text { and }-2
\)
So, the points \( x=-1 \) and \( x=-2 \) divides the real line into two disjoint intervals,
\(
(-\infty,-2),(-2,-1) \text { and }(-1, \infty)
\)
So, in interval \( (-\infty,-2),(-1, \infty) \)
\(
f^{\prime}(x)=-6(x+1)(x+2) < 0
\)
Therefore, the given function (f) is strictly decreasing for \( x < -2 \) and \( x > - \) 1 .
So, in interval \( (-2 .-1) \)
\(
f^{\prime}(x)=-6(x+1)(x+2) > 0
\)
Therefore, the given function (f) is strictly increasing for \( -2 < x < -1 \).

It is given that function \( f(x)=6-9 x-x^{2} \)
\(
f^{\prime}(x)=-9-2 x
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
\Rightarrow x=\frac{-9}{2}
\)
So, the point \( x=\frac{-9}{2} \) divides the real line into two disjoint intervals, \( \left(-\infty, \frac{-9}{2}\right) \) and \( \left(\frac{-9}{2}, \infty\right) \)
So, in interval \( \left(-\infty, \frac{-9}{2}\right) \)
\(
f^{\prime}(x)=-9-2 x > 0
\)
Therefore, the given function (f) is strictly increasing for \( x < \frac{-9}{2} \).
And in interval \( \left(\frac{-9}{2}, \infty\right) \)
\(
f^{\prime}(x)=-9-2 x < 0
\)
Therefore, the given function (f) is strictly decreasing for \( x > \frac{-9}{2} \).
Thus, f is strictly decreasing for \( x > \frac{-9}{2} \).

It is given that function \( \mathrm{f}(x)=-(x+1)^{3}(x-3)^{3} \)
\(
\Rightarrow \mathrm{f}^{\prime}(x)=3(x+1)^{2}(x-3)^{3}+3(x+1)^{3}(x-3)^{2}\)
\(\Rightarrow \mathrm{f}^{\prime}(x)=3(x+1)^{2}(x-3)^{2}[x-3+x+1]\)
\(\Rightarrow \mathrm{f}^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1)
\)
If \( f^{\prime}(x)=0 \), then we get,
\(
\Rightarrow x=-1,3 \text { and } 1
\)
So, the points \( x=-1, x=1 \) and \( x=3 \) divides the real line into four disjoint
intervals,
\(
(-\infty,-1),(-1,1),(-1,3) \text { and }(3, \infty)
\)
So, in interval \( (-\infty,-1),(-1,1) \)
\(
f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1) < 0
\)
Therefore, the given function (f) is strictly decreasing in intervals \( (-\infty,-1),(-1,1) \).
So, in interval \( (1,3) \) and \( (3, \infty) \)
\(
f^{\prime}(x)=6(x+1)^{2}(x-3)^{2}(x-1) > 0
\)
Therefore, the given function (f) is strictly increasing in intervals \( (1,3) \) and \( (3, \infty) \).

Let \( y=\log (1+x)-\frac{2 x}{2+x} \)
\( \Rightarrow \frac{d y}{d x}=\frac{1}{1+x}-\frac{(2+x) \cdot 2-2 \times(1)}{(2+x)^{2}} \)
\( \Longrightarrow \frac{1}{1+x}-\frac{4+2 x-2 x}{(2+x)^{2}}=\frac{1}{1+x}-\frac{4}{(2+x)^{2}} \)
\( =\frac{(2+x)^{2}-4(1+x)}{(1+x)(2+x)^{2}} \)
\( =\frac{\left(4+x^{2}+4 x\right)-(4-4 x)}{(1+x)(2+x)^{2}} \)
\( =\frac{x^{2}}{(1+x)(2+x)^{2}} \)
\( =\frac{d y}{d x}=\frac{1}{1+x}\left(\frac{x}{2+x}\right)^{2} \)
Now, \( x > -1 \)
\( \Rightarrow 1+x > 0 \)
Also, for all \( x > -1, \frac{x}{x+2 x} > 0 \)
\( \Rightarrow \frac{d y}{d x}=\frac{1}{1+x}\left(\frac{x}{2+x}\right)^{2} > \) for \( x > -1 \)
Therefore, \( f \) is an increasing function throughout its domain.

It is given that \( y=[x(x-2)]^{2} \), then,
\(
\frac{d y}{d x}=y^{\prime}=2\left(x^{2}-2 x\right)(2 x-2)\)
\(=4 x(x-2)(x-1)
\)
Now if \( \frac{d y}{d x}=0 \)
\(
\Rightarrow x=0,1,2
\)
So, the points \( x=0, x=1 \) and \( x=2 \) divides the real line into four disjoint intervals,
\(
(-\infty, 0),(0,1),(1,2) \text { and }(2, \infty)
\)
So, in interval \( (-\infty, 0),(1,2) \)
\(
\frac{d y}{d x} < 0
\)
Therefore, the given function (f) is strictly decreasing in intervals (\( \infty, 0),(1,2) \)
So, in interval \( (0,1) \) and \( (2, \infty) \)
\(
\frac{d y}{d x} > 0
\)
Therefore, the given function (f) is strictly increasing for \( 0 < x < 1 \) and \( x > 2 \)

We have, \( y=\frac{4 \sin \theta}{(2+\cos \theta)}-\theta \)
\(
\therefore \frac{d y}{d x}=\frac{(2+\cos \theta)(4 \cos \theta)-4 \sin \theta(-\sin \theta)}{(2+\cos \theta)^{2}}-1\)
\(=\frac{8 \cos \theta+4 \cos ^{2} \theta-4 \sin \theta(-\sin \theta)}{(2+\cos \theta)^{2}}-1
\)
\(
=\frac{8 \cos \theta+4 \cos ^{2} \theta+4 \sin ^{2} \theta}{(2+\cos \theta)^{2}}-1\)
\(=\frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}-1
\)
Now, \( \frac{d y}{d x}=0 \)
\(
\Rightarrow \frac{8 \cos \theta+4}{(2+\cos \theta)^{2}}=1\)
\(\Rightarrow 8 \cos \theta+4=4+\cos ^{2} \theta+4 \cos \theta\)
\(\Rightarrow \cos ^{2} \theta-4 \cos \theta=0\)
\(\Rightarrow \cos \theta(\cos \theta-4)=0\)
\(\Rightarrow \cos \theta=0 \text { or } \cos \theta=4
\)
Since, \( \cos \theta \neq 0 \Longrightarrow \theta=\frac{\pi}{2} \)
\(
\Longrightarrow \cos \theta=0 \Longrightarrow \theta=\frac{\pi}{2}
\)
Now, \( \frac{d y}{d x}=\frac{8 \cos \theta+4-\left(4 \cos ^{2} \theta+4 \sin ^{2} \theta\right)}{(2+\cos \theta)^{2}} \)
\(
=\frac{4 \cos \theta-\cos ^{2} \theta}{(2+\cos \theta)^{2}}\)
\(=\frac{4 \cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}}
\)
In interval, \( \left(0, \frac{\pi}{2}\right) \), we have \( \cos \theta > 0 \). Also, \( 4 > \cos \theta \)
\(
\Rightarrow 4-\cos \theta > 0
\)
Therefore, \( \cos \theta(4-\cos \theta) > 0 \) and also \( (2+\cos \theta)^{2} > 0 \)
\(
\Rightarrow \frac{\cos \theta(4-\cos \theta)}{(2+\cos \theta)^{2}} > 0\)
\(\Rightarrow \frac{d y}{d x} > 0
\)
Therefore, \(y\) is strictly increasing in interval \( \left(0, \frac{\pi}{2}\right) \).
Also, the given function is continuous at \( x=0 \) and \( x=\frac{\pi}{2} \).
Therefore, \(y\) is increasing in interval \( \left[0, \frac{\pi}{2}\right] \).

The given function is \( f(x)=\log x \)
\(
\Rightarrow f^{\prime}=\frac{1}{x}
\)
It is clear that for \( x > 0, f^{\prime}=\frac{1}{x} > 0 \)
Therefore, \( \mathrm{f}(x)=\log x \) is strictly increasing in interval \( (0, \infty) \).

It is given that function \( f(x)=x^{2}-x+1 \)
\( \mathrm{f}^{\prime}(x)=2 x-1 \)
If \( f^{\prime}(x)=0 \), then we get,
\( \Rightarrow x=\frac{1}{2} \)
So, the point \( x=\frac{1}{2} \) divides the interval \( (-1,1) \) into two disjoint intervals, \( \left(-1, \frac{1}{2}\right) \) and \( \left(\frac{1}{2}, 1\right) \)
So, in interval \( \left(-1, \frac{1}{2}\right) \)
\( \mathrm{f}^{\prime}(x)=2 x-1 < 0 \)
Therefore, the given function (f) is strictly decreasing in interval \( \left(-1, \frac{1}{2}\right) \)
So, in interval \( \left(\frac{1}{2}, 1\right) \).
\(
\mathrm{f}^{\prime}(x)=2 x-1 > 0
\)
Therefore, the given function (f) is strictly increasing in interval for \( \left(\frac{1}{2}, 1\right) \)
Therefore, \( f \) is neither strictly increasing and decreasing in interval (\( 1,1) \).

(A) Let \( \mathrm{f}_{1}(x)=\cos x \)
\(
\therefore f_{1}^{\prime}=-\sin x
\)
In interval \( \left(0, \frac{\pi}{2}\right), f_{1}^{\prime}=-\sin x < 0 \).
Therefore, \( f_{1}(x)=\cos x \) is strictly decreasing in interval \( \left(0, \frac{\pi}{2}\right) \).
(B) Let \( \mathrm{f}_{2}(x)=\cos 2 x \)
\(
\therefore f_{2}^{\prime}(x)=-2 \sin 2 x
\)
Now, \( 0 < x < \frac{\pi}{2} \)
\(
\begin{array}{l}
\Rightarrow 0 < 2 x < \pi \\
\Rightarrow \sin 2 x > 0 \\
\Rightarrow-2 \sin 2 x < 0
\end{array}
\)
\(
\therefore f_{2}^{\prime}(x)=-2 \sin 2 x < 0 \text { on }\left(0, \frac{\pi}{2}\right)
\)
Therefore, \( f_{2}(x)=\cos 2 x \) is strictly decreasing in interval \( \left(0, \frac{\pi}{2}\right) \).
(C) Let \( \mathrm{f}_{3}(x)=\cos 3 x \)
\(
\therefore f_{3}^{\prime}(x)=-3 \sin 3 x
\)
Now, \( f_{3}^{\prime}=0 \)
\( \Rightarrow \sin 3 x=0 \)
\( \Rightarrow 3 x=\pi \), as \( x \in\left(0, \frac{\pi}{2}\right) \)
\(
\Rightarrow x=\frac{\pi}{3}
\)
The point \( x=\frac{\pi}{3} \) divides the interval \( \left(0, \frac{\pi}{2}\right) \) into two distinct intervals.
i.e. \( \left(0, \frac{\pi}{3}\right) \) and \( \left(\frac{\pi}{3}, \frac{\pi}{2}\right) \)
Now, in interval \( \left(0, \frac{\pi}{3}\right) \),
\( \mathrm{f}_{3}^{\prime}(x)=-3 \sin 3 x < 0 \) as \( \left(0 < x < \frac{\pi}{2} \Rightarrow 0 < 3 x < \pi\right) \)
Therefore, \( f_{3} \) is strictly decreasing in interval \( \left(0, \frac{\pi}{3}\right) \).
Now, in interval \( \left(\frac{\pi}{3}, \frac{\pi}{2}\right) \).
\(
f_{3}^{\prime}(x)=-3 \sin 3 x > 0 \text { as } \frac{\pi}{3} < x < \frac{\pi}{3} \Rightarrow \pi < 3 x < \frac{3 \pi}{2}
\)
Therefore, \( \mathrm{f}_{3} \) is strictly increasing in interval \( \left(\frac{\pi}{3}, \frac{\pi}{2}\right) \).
(D) Let \( \mathrm{f}_{4}=\tan x \)
\( \therefore \mathrm{f}_{3}{ }^{\prime}(x)=\sec ^{2} x \)
In interval \( \left(0, \frac{\pi}{2}\right) \),
\(
f_{3}^{\prime}=\sec ^{2} x > 0
\)
Therefore, f 4 is strictly increasing in interval \( \left(0, \frac{\pi}{2}\right) \).

It is given that \( f(x)=x^{100}+\sin x-1 \)
Then, \( f^{\prime}(x)=100 x^{99}+\cos x \)
In interval \( (0,1), \cos x > 0 \) and \( 100 x^{99} > 0 \)
\(
\Rightarrow \mathrm{f}^{\prime}(x) > 0
\)
Therefore, function f is strictly increasing in interval \( (0,1) \).
In interval \( \left(\frac{\pi}{2}, \pi\right), \cos x < 0 \) and \( 100 x^{99} > 0 \).
Also, \( 100 x^{99} > \cos x \)
\(
\Rightarrow \mathrm{f}^{\prime}(x) > 0 \text { in }\left(\frac{\pi}{2}, \pi\right)
\)
Therefore, function f is strictly increasing in interval \( \left(\frac{\pi}{2}, \pi\right) \).
In interval \( \left(0, \frac{\pi}{2}\right), \cos x < 0 \) and \( 100 x^{99} > 0 \).
Also, \( 100 x^{99} > \cos x \)
\(
\Rightarrow \mathrm{f}^{\prime}(x) > 0 \text { on }\left(0, \frac{\pi}{2}\right)
\)
Therefore, function f is strictly increasing in interval \( \left(0, \frac{\pi}{2}\right) \).
Hence, function f is strictly decreasing on none of the intervals.

It is given that function \( f(x)=x^{2}+a x+1 \)
\(
f^{\prime}(x)=2 x+a
\)
Now, function f will be increasing in \( [1,2] \),
\(
\text { if } f^{\prime}(x) > 0 \text { in }[1,2]\)
\(\Rightarrow 2 x+a > 0\)
\(\Rightarrow 2 x > -a
\)
\(
\Rightarrow \mathrm{a} < -2 x
\)
Therefore, we have to find the least value of a such that
\(
\Rightarrow \mathrm{a} < -2 x \text { when } x \in[1,2]
\)
Now, \( 1 \leq x \leq 2 \)
\(
\Rightarrow-4 \leq-2 x \leq-2
\)
Therefore, the least value of a for \( f \) to be increasing on \( [1,2] \) is given by
\(
\Rightarrow \mathrm{a}=-4
\)
Therefore, the least value of a is -4 .

It is given that \( f(x)=x+\frac{1}{x} \)
\(
\therefore \mathrm{f}^{\prime}(x)=1-\frac{1}{x^{2}}
\)
Now, \( \mathrm{f}^{\prime}(x)=0 \)
\(
\Rightarrow x= \pm 1
\)
The points \( x=1 \) and \( x=-1 \) divide the real line in three disjoint intervals \( (-\infty,-1),(-1,1) \) and \( (1, \infty) \)
Now in interval, \( (-1,1) \)
it is clear that \( -1 < x < 1 \)
\(
\Rightarrow x^{2} < 1
\)
\(
\Rightarrow 1-\frac{1}{x^{2}} < 0, x \neq 0\)
Therefore, \( \mathrm{f}^{\prime}(x)=1-\frac{1}{x^{2}} < 0(-1,1) \sim\{0\} \)
Therefore, f is strictly decreasing on \( (-1,1) \sim\{0\} \)
\(
x < -1 \text { or } 1 < x\)
\(\Rightarrow x^{2} > 1\)
\(\Rightarrow 1-\frac{1}{x^{2}}\)
\(\Rightarrow 1-\frac{1}{x^{2}} > 0
\)
Therefore, \( \mathrm{f}^{\prime}(x)=1-\frac{1}{x^{2}} > 0(-\infty,-1) \) and \( (1, \infty) \)
Therefore, fis strictly increasing in interval I disjoint from ( \( -1,1 \) ) Hence Proved.

It is given that \( \mathrm{f}(x)=\log \sin x \)
\( \Rightarrow f^{\prime}(x)=\frac{1}{\sin x} \cos x=\cot x \)
In interval \( \left(0, \frac{\pi}{2}\right), \mathrm{f}^{\prime}(x)=\cot x > 0 \)
Therefore, f is strictly increasing in \( \left(0, \frac{\pi}{2}\right) \).
In interval \( \left(\frac{\pi}{2}, \pi\right), \mathrm{f}^{\prime}(x)=\cot x < 0 \)
Therefore, f is strictly decreasing in \( \left(\frac{\pi}{2}, \pi\right) \).

It is given that \( f(x)=\log |\cos x| \)
\( \Rightarrow f^{\prime}(x)=\frac{1}{\cos x}(-\sin x)=-\tan x \)
In interval \( \left(0, \frac{\pi}{2}\right), \mathrm{f}^{\prime}(x)=-\tan x < 0 \)
Therefore, f is strictly decreasing on \( \left(0, \frac{\pi}{2}\right) \).
In interval \( \left(\frac{3 \pi}{2}, 2 \pi\right), \mathrm{f}^{\prime}(x)=-\tan x > 0 \)
Therefore, f is strictly increasing in \( \left(\frac{3 \pi}{2}, 2 \pi\right) \).

We have, \( f(x)=x^{3}-3 x^{2}+3 x-100 \)
\(
\Rightarrow f^{\prime}(x)=3 x^{2}-6 x+3\)
\(=3\left(x^{2}-2 x+1\right)
\)
\(
=3(x-1) 2
\)
For any \( x \in \mathrm{R},(x-1) 2 > 0 \)
Thus, \( f^{\prime}(x) \) is always positive in \( R \).
Therefore, the given function ( \( f \) ) is increasing in \( R \).

it is given that \( y=x^{2} \mathrm{e}^{-x} \) then \( \frac{d y}{d x}=2 x e^{-x}-x^{2} e^{-x}=x e^{-x}(2-x) \)
Now if \( \frac{d y}{d x}=0 \)
\( \Rightarrow x=0 \) and \( x=2 \)
The points \( x=0 \) and \( x=2 \) divide the real line into three disjoint intervals ie, \( (-\infty, 0),(0,2) \) and \( (2, \infty) \).
In interval \( (-\infty, 0) \) and \( (2, \infty) \),
\( \mathrm{f}^{\prime}(x) < 0 \) as \( \mathrm{e}^{-x} \) is always positive.
Therefore, fis decreasing on \( (-\infty, 0) \) and \( (2, \infty) \).
In interval \( (0,2), \mathrm{f}^{\prime}(x) > 0 \)
Therefore, f is strictly increasing in interval (0.2).