CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

NCERT Class 10 Mathematics Chapter 6: Triangle – For Free. || Get the complete NCERT Solutions for Class 10 Maths Chapter 6: Triangle, covering Exercise 6.3. This free resource helps you understand key concepts and solve problems with ease, perfect for Class 10 students preparing for exams using NCERT Maths materials. We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangle Exercise 6.3 help you. If you have any queries regarding NCERT Maths Solutions Chapter 6 Triangle Exercise 6.3, drop a comment below, and we will get back to you at the earliest.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)
Exercise - 6.3

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

(i) State which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Answer

(i) From the figure:
$\angle \mathrm{A}=\angle \mathrm{P}=60^{\circ}$
$\angle \mathrm{B}=\angle \mathrm{Q}=80^{\circ}$
$\angle \mathrm{C}=\angle \mathrm{R}=40^{\circ} $
Therefore, $ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $ [By AAA similarity]
Now corresponding sides of triangles will be proportional,
$ \frac{A B}{Q R}=\frac{B C}{R P}=\frac{C A}{P Q} $

(ii) State which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Answer

From the triangle, $ \frac{A B}{Q R}=\frac{B C}{P R}=\frac{A C}{P Q}=0.5 $
Hence the corresponding sides are propotional. Thus the corresponding angles will be equal. The triangles $ A B C $ and $ Q R P $ are similar to each other by SSS similarity

(iii) State which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Answer

The given triangles are not similar because the corresponding sides are not proportional

(iv) State which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Answer

In triangle MNL and QPR, we have $ \angle M=\angle Q=70^{\circ} $
But $\frac{M N}{P Q}=\frac{2.5}{6}=\frac{5}{12}$
$\frac{M L}{P R}=\frac{5}{10}=\frac{1}{2}$
$\Rightarrow \frac{M N}{P Q} \neq \frac{M L}{P R} $
Therefore, MNL and QPR are not similar.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

(v) State which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Answer

In triangle $ A B C $ and $ D E F $, we have $\mathrm{AB}=2.5, \mathrm{BC}=3$
$\angle \mathrm{A}=80^{\circ}$
$\mathrm{EF}=6$
$\mathrm{DF}=5$
$\angle \mathrm{F}=80^{\circ}$
$\frac{A B}{D F}=\frac{2.5}{5}=\frac{1}{2} $
And, $ \frac{B C}{E F}=\frac{3}{6}=\frac{1}{2} $
$ \angle \mathrm{B} \neq \angle \mathrm{F} $
Hence, triangle ABC and DEF are not similar

(vi) State which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Answer

In triangle DEF, we have
$ \angle \mathrm{D}+\angle \mathrm{E}+\angle \mathrm{F}=180^{\circ} $ (Sum of angles of triangle)
$70^{\circ}+80^{\circ}+\angle \mathrm{F}=180^{\circ}$
$\angle \mathrm{F}=30^{\circ} $
In $ P Q R $, we have
$\angle \mathrm{P}+\angle \mathrm{Q}+\angle \mathrm{R}=180^{\circ}$
$\angle \mathrm{P}+80^{\circ}+30^{\circ}=180^{\circ}$
$\angle \mathrm{P}=70^{\circ} $
In triangle DEF and $ P Q R $, we have
$\angle \mathrm{D}=\angle \mathrm{P}=70^{\circ}$
$\angle \mathrm{F}=\angle \mathrm{Q}=80^{\circ} $
$ \angle \mathrm{F}=\angle \mathrm{R}=30^{\circ} $
Hence, $ \triangle \mathrm{DEF} \sim \triangle \mathrm{PQR} $ (AAA similarity)

2. In Fig. 6.35, $ \Delta \mathrm{ODC} \sim \Delta \mathrm{OBA}, \angle \mathrm{BOC}=125^{\circ} $ and $ \angle \mathrm{CDO}=70^{\circ} $. Find $ \angle \mathrm{DOC}, \angle \mathrm{DCO} $ and $ \angle \mathrm{OAB} $

Answer

From the figure,

We see, DOB is a straight line
$ \angle \mathrm{DOC}+\angle \mathrm{COB}=180^{\circ} $ (angles on a straight line form a supplementary pair)
$ \angle \mathrm{DOC}=180^{\circ}-125^{\circ}$
$\angle \mathrm{DOC}=55^{\circ} $
Now, In $ \triangle \mathrm{DOC} $,
$ \angle \mathrm{DCO}+\angle \mathrm{CDO}+\angle \mathrm{DOC}=180^{\circ} $
(Sum of the measures of the angles of a triangle is $ 180^{\circ} $ )
$\angle \mathrm{DCO}+70^{\circ}+55^{\circ}=180^{\circ}$
$\angle \mathrm{DCO}=55^{\circ} $
It is given that $ \Delta \mathrm{ODC} \sim \Delta \mathrm{OBA} $
$ \angle \mathrm{OAB}=\angle \mathrm{OCD} $ (Corresponding angles are equal in similar triangles)
Thus, $ \angle \mathrm{OAB}=55^{\circ} $.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

3. Diagonals AC and BD of a trapezium ABCD with $ \mathrm{AB} \| \mathrm{DC} $ intersect each other at the point $ O $. Show that $ \frac{A O}{B O}=\frac{C O}{D O} $.

Answer

In $ \triangle \mathrm{DOC} $ and $ \triangle \mathrm{BOA} $,
$ \angle \mathrm{CDO}=\angle \mathrm{ABO} $ (Alternate interior angles as $ \mathrm{AB} \| \mathrm{CD}) $
$ \angle \mathrm{DCO}=\angle \mathrm{BAO} $ (Alternate interior angles as $ \mathrm{AB} \| \mathrm{CD} ) $
$ \angle \mathrm{DOC}=\angle \mathrm{BOA} $ (Vertically opposite angles)
Therefore,
$ \triangle \mathrm{DOC} \sim \triangle \mathrm{BOA}\quad $ [BY AAA similarity] Now in similar triangles, the ratio of corresponding sides are proportional to each other. Therefore, $ \frac{O A}{O C}=\frac{O B}{O D} \quad\ldots$(Corresponding sides are proportional)
or $ \frac{A O}{C O}=\frac{B O}{D O} $
Hence proved.

4. In Fig. 6.36, $ \frac{Q R}{Q S}=\frac{Q T}{P R} $ and $ < 1= < 2 $. Show that $ \Delta P Q S \sim \Delta T Q R $.

Answer

To Prove: $ \triangle \mathrm{PQS} \sim \triangle \mathrm{TQR} $
Given: In $ \triangle \mathrm{PQR} $,
$ \angle \mathrm{PQR}=\angle \mathrm{PRQ} $
Proof: As $ \angle \mathrm{PQR}=\angle \mathrm{PRQ} $
$ \mathrm{PQ}=\mathrm{PR} $ [sides opposite to equal angles are equal] (i)
Given,
$ \frac{Q R}{Q S}=\frac{Q T}{P R} $
$ \frac{Q R}{Q S}=\frac{Q T}{Q P} $ by (1)
In $ \triangle \mathrm{PQS} $ and $ \triangle \mathrm{TQR} $,
we get
$\frac{Q R}{Q S}=\frac{Q T}{Q P}$
$\angle \mathrm{Q}=\angle \mathrm{Q} $
Therefore,
By SAS similarity Rule which states that Triangles are similar if two sides in one triangle are in the
same proportion to the corresponding sides in the other, and the included angle are equal.
$ \triangle \mathrm{PQS} \sim \triangle \mathrm{TQR} $
Hence, Proved.

5. S and T are points on sides PR and QR of $ \triangle \mathrm{PQR} $ such that $ \angle \mathrm{P}= \angle RTS$. Show that $ \triangle \mathrm{RPQ} \sim \triangle \mathrm{RTS} $

Answer

In $ \triangle \mathrm{RPQ} $ and $ \triangle \mathrm{RST} $,
$ \angle \mathrm{RTS}=\angle \mathrm{QPS} $ (Given)
$ \angle \mathrm{R}=\angle \mathrm{R} $ (Common to both the triangles)
If two angles of two triangles are equal, third angle will also be equal.
As the sum of interior angles of triangle is constant and is $ 180^{\circ} $

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

$ \therefore \triangle \mathrm{RPQ} \sim \triangle \mathrm{RTS} $ (By AAA similarity).

6. In Fig. 6.37, if $ \triangle \mathrm{ABE} \cong \triangle \mathrm{ACD} $, show that $ \triangle \mathrm{ADE} \sim \triangle \mathrm{ABC} $.

Answer

To Prove: $ \triangle \mathrm{ADE} \sim \Delta \mathrm{ABC} $
Given: $ \triangle \mathrm{ABE} \cong \triangle \mathrm{ACD} $
Proof: $ \triangle \mathrm{ABE} \cong \triangle \mathrm{ACD} $
$ \therefore \mathrm{AB}=\mathrm{AC} \quad(\mathrm{By} \mathrm{~CPCT}) $ (i)
And,
$ \mathrm{AD}=\mathrm{AE}\quad(\mathrm{By} \mathrm{~CPCT}) $ (ii)
In $ \triangle \mathrm{ADE} $ and $ \triangle \mathrm{ABC} $,
Dividing equation (ii) by (i)
$ \frac{A B}{A D}=\frac{A C}{A E} $
$ \angle \mathrm{A}=\angle \mathrm{A} $ (Common)
SAS Similarity: Triangles are similar if two sides in one triangle are in the same proportion to the corresponding sides in the other, and the included angle are equal.
Therefore,
$ \triangle \mathrm{ADE} \sim \triangle \mathrm{ABC} $ (By SAS similarity)
Hence, Proved.

(i) In Fig. 6.38, altitudes AD and CE of $ \triangle \mathrm{ABC} $ intersect each other at the point $ P $.
Show that:
$ \triangle AEP \sim \triangle CDP $

Answer

In $ \triangle \mathrm{AEP} $ and $ \triangle \mathrm{CDP} $,
$ \angle \mathrm{AEP}=\angle \mathrm{CDP}\left(\right. $ Each $ \left.90^{\circ}\right) $
$ \angle \mathrm{APE}=\angle \mathrm{CPD} $ (Vertically opposite angles)
Hence, by using AA similarity,
$ \triangle \mathrm{AEP}\sim\Delta \mathrm{CDP} $

(ii) In Fig. 6.38, altitudes AD and CE of $ \triangle \mathrm{ABC} $ intersect each other at the point $ P $.
Show that:
$ \triangle \mathrm{ABD} \sim \triangle \mathrm{CBE} $

Answer

In $ \triangle \mathrm{ABD} $ and $ \triangle \mathrm{CBE} $,
$ \angle \mathrm{ADB}=\angle \mathrm{CEB}\left(\right. $ Each $ \left.90^{\circ}\right) $
$ \angle \mathrm{ABD}=\angle \mathrm{CBE} $ (Common) Hence, by using AA similarity,
$ \Delta \mathrm{ABD}{ }\sim \Delta \mathrm{CBE} $

(iii) In Fig. 6.38, altitudes AD and CE of $ \triangle \mathrm{ABC} $ intersect each other at the point $ P $.
Show that:
$ \triangle \mathrm{AEP} \sim \triangle \mathrm{ADB} $

Answer

In $ \triangle \mathrm{AEP} $ and $ \triangle \mathrm{ADB} $,
$ \angle \mathrm{AEP}=\angle \mathrm{ADB}\left(\right. $Each $ \left.90^{\circ}\right) $
$ \angle \mathrm{PAE}=\angle \mathrm{DAB} $ (Common)
Hence, by using AA similarity,
$ \triangle \mathrm{AEP}\sim \triangle \mathrm{ADB} $

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

$Mathninja.in$

(iv) In Fig. 6.38, altitudes AD and CE of $ \triangle \mathrm{ABC} $ intersect each other at the point $ P $.
Show that:
$ \triangle \mathrm{PDC} \sim \triangle \mathrm{BEC} $

Answer

In $ \triangle \mathrm{PDC} $ and $ \triangle \mathrm{BEC} $,
$ \angle \mathrm{PDC}=\angle \mathrm{BEC}\left(\right. $ Each $ \left.90^{\circ}\right) $
$ \angle \mathrm{PCD}=\angle \mathrm{BCE} $ (Common angle)
Hence, by using AA similarity,
$ \triangle \mathrm{PDC} \sim \triangle \mathrm{BEC} $

8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that $ \triangle \mathrm{ABE} \sim \triangle \mathrm{CFB} $.

Answer

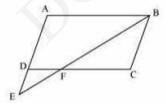
To Prove: $ \triangle \mathrm{ABE} \sim \triangle\mathrm{CFB} $
Given: E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F . As shown in the figure.
Proof:
In $ \triangle \mathrm{ABE} $ and $ \triangle \mathrm{CFB} $,
$ \angle \mathrm{A}=\angle \mathrm{C}\quad $ (Opposite angles of a parallelogram are equal)
$ \angle \mathrm{AEB}=\angle \mathrm{CBF} \quad$ (Alternate interior angles are equal because $ \mathrm{AE} \| \mathrm{BC}) $
Therefore,
$ \triangle \mathrm{ABE} \sim \triangle \mathrm{CFB} $ (By AA similarity)
Hence, Proved.

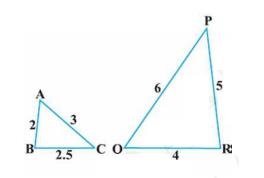
(i) In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
$ \triangle \mathrm{ABC} \sim \triangle \mathrm{AMP} $

Answer

(i) To Prove: $ \triangle \mathrm{ABC} \sim \triangle \mathrm{AMP} $
Given: In $ \triangle \mathrm{ABC} $ and $ \triangle \mathrm{AMP} $,
$ \angle \mathrm{ABC}=\angle \mathrm{AMP}\left(\right. $Each $ \left.90^{\circ}\right) $
Proof:
$ \angle \mathrm{ABC}=\angle \mathrm{AMP}\left(\right. $Each $ \left.90^{\circ}\right) $
$ \angle \mathrm{A}=\angle \mathrm{A} \ ( $Common)
$ \therefore \triangle \mathrm{ABC} \sim \triangle \mathrm{AMP} $ (By AA similarity)
Hence, Proved.

(ii) In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
$ \frac{C A}{P A}=\frac{B C}{M P} $

Answer

$ \triangle \mathrm{ABC} \sim \triangle \mathrm{AMP} $
Now we get that, Similarity Theorem - If the lengths of the corresponding sides of two triangles are proportional, then the triangles must be similar. And the converse is also true, so we have $ \frac{C A}{P A}=\frac{B C}{M P} $
Hence, Proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

10. CD and GH are respectively the bisectors of $ \angle \mathrm{ACB} $ and $ \angle \mathrm{EGF} $ in such a way that D and H lie on sides AB and FE of $ \triangle \mathrm{ABC} $ and $ \triangle \mathrm{EFG}$ respectively. If $ \triangle \mathrm{ABC} \sim \triangle \mathrm{FEG} $, show that:
(i) $ \frac{C D}{G H}=\frac{A C}{F G} $
(ii) $ \triangle DCB \sim \triangle HGE$
(iii) $ \triangle \mathrm{DCA} \sim \triangle \mathrm{HGF} $

Answer

Given, $ \triangle \mathrm{ABC} \sim \triangle\mathrm{FEG} \ldots \ldots (1) $
$ \Rightarrow $ corresponding angles of similar triangles
$ \Rightarrow \angle \mathrm{BAC}=\angle \mathrm{EFG} \ldots (2) $
And $ \angle \mathrm{ABC}=\angle \mathrm{FEG} \ldots \ldots (3) $
$\Rightarrow \angle \mathrm{ACB}=\angle \mathrm{FGE}$
$\Rightarrow \frac{1}{2} < A C B=\frac{1}{2} < F G E $
$ \Rightarrow \angle \mathrm{ACD}=\angle \mathrm{FGH} $ and $ \angle \mathrm{BCD}=\angle \mathrm{EGH} \ldots \ldots(4) $
Consider $ \triangle \mathrm{ACD} $ and $ \triangle \mathrm{FGH} $
$ \Rightarrow $ From eq(2) we have
$ \Rightarrow \angle \mathrm{DAC}=\angle \mathrm{HFG} $
$ \Rightarrow $ From eq(4) we have
$ \Rightarrow \angle \mathrm{ACD}=\angle \mathrm{EGH} $
Also, $ \angle \mathrm{ADC}=\angle \mathrm{FGH} $
$ \Rightarrow $ If the 2 angle of triangle are equal to the 2 angle of another triangle, then by angle sum property of triangle 3rd angle will also be equal.
$ \Rightarrow $ by AAA similarity we have in two triangles if the angles are equal, then sides opposite to the equal angles are in the same ratio (or proportional) and hence the triangles are similar.
$ \therefore \triangle \mathrm{ADC} \sim \triangle \mathrm{FHG} $
$ \Rightarrow $ By Converse proportionality theorem
$ \Rightarrow \frac{C D}{G H}=\frac{A C}{F G} $
Consider $ \triangle \mathrm{DCB} $ and $ \triangle \mathrm{HGE} $
From eq(3) we have
$ \Rightarrow \angle \mathrm{DBC}=\angle \mathrm{HEG} $
$ \Rightarrow $ From eq(4) we have
$ \Rightarrow \angle \mathrm{BCD}=\angle \mathrm{FGH} $
Also, $ \angle \mathrm{BDC}=\angle \mathrm{EHG} $
$ \therefore \triangle \mathrm{DCB} \sim \triangle \mathrm{HGE} $
Hence proved.

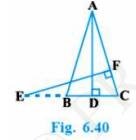
11. In Fig. 6.40, $ E $ is a point on side CB produced of an isosceles triangle ABC with $ \mathrm{AB}=\mathrm{AC} $. If $ \mathrm{AD} \perp \mathrm{BC} $ and $ \mathrm{EF} \perp \mathrm{AC} $, prove that $ \triangle \mathrm{ABD} \sim \triangle \mathrm{ECF} $

Answer

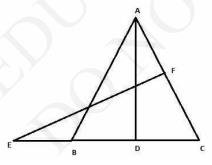
To Prove: $ \triangle \mathrm{ABD} \sim \triangle \mathrm{ECF} $
Given: ABC is an isosceles triangle, AD is perpendicular to BC BC is produced to E and EF is perpendicular to AC
Proof:
Given that ABC is an isosceles triangle
$\mathrm{AB}=\mathrm{AC}$
$\Rightarrow \angle \mathrm{ABD}=\angle \mathrm{ECF} $
In $ \triangle \mathrm{ABD} $ and $ \triangle \mathrm{ECF} $,
$ \angle \mathrm{ADB}=\angle \mathrm{EFC}\left(\right. $Each $ \left.90^{\circ}\right) $
$ \angle \mathrm{ABD}=\angle \mathrm{ECF} $ (Proved above)
Therefore,
$ \triangle \mathrm{ABD} \sim \triangle \mathrm{ECF} $ (By using AA similarity criterion)
AA Criterion: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
Hence, Proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

$Mathninja.in$

12. Sides $ A B $ and $ B C $ and median $ A D $ of a triangle $ A B C $ are respectively proportional to sides PQ and QR and median PM of $ \triangle \mathrm{PQR} $ (see Fig. 6.41). Show that $ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $.

Answer

To Prove: $ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $
Given:
$\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A D}{P M}$
Proof: Median divides the opposite side
$ B D=\frac{B C}{2} $ and,
$ Q M=\frac{Q R}{2} $
Now,
$ \frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A D}{P M} $
Multiplying and dividing by 2, we get
$\frac{A B}{P Q}=\frac{\frac{2}{2 B C}}{\frac{1}{2 Q R}}=\frac{A D}{P M}$
$\frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M} $
In $ \triangle \mathrm{ABD} $ and $ \triangle \mathrm{PQM} $,
$ \frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M} $
Side-Side-Side (SSS) Similarity Theorem - If the lengths of the corresponding sides of two triangles are proportional, then the triangles must be similar.
$ \triangle \mathrm{ABD} \sim \triangle \mathrm{PQM} $ (By SSS similarity)
$ \angle \mathrm{ABD}=\angle \mathrm{PQM} $ (Corresponding angles of similar triangles)
In $ \triangle \mathrm{ABC} $ and $ \triangle \mathrm{PQR} $,
$ \angle \mathrm{ABD}=\angle \mathrm{PQM} $ (Proved above)
$ \frac{A B}{P Q}=\frac{B C}{Q R} $
The SAS Similarity Theorem states that if two sides in one triangle are proportional to two sides in another triangle and the included angle in both are congruent, then the two triangles are similar.
$ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $ (By SAS similarity)
Hence, Proved.

13. D is a point on the side BC of a triangle ABC such that $ \angle \mathrm{ADC} $ $ =\angle \mathrm{BAC} $. Show that $ \mathrm{CA}^{2}=\mathrm{CB} . \mathrm{CD} $

Answer

In $ \triangle \mathrm{ADC} $ and $ \triangle \mathrm{BAC} $,

To Prove: $ \mathrm{C A}^{2}=\mathrm{C B} . \mathrm{C D} $
Given: $ \angle A D C=\angle B A C $
Proof: Now In $ \triangle \mathrm{ADC} $ and $ \triangle \mathrm{BAC} $,
$ \angle \mathrm{ADC}=\angle \mathrm{BAC} $
$ \angle \mathrm{ACD}=\angle \mathrm{BCA} $ (Common angle)
According to AA similarity, if two corresponding angles of two
triangles are equal then the triangles are similar
$ \triangle \mathrm{ADC} \sim \triangle \mathrm{BAC} $ (By AA similarity)
We know that corresponding sides of similar triangles are in proportion
Hence in $ \triangle \mathrm{ADC} $ and $ \triangle \mathrm{BAC} $,
$ \frac{C A}{C B}=\frac{C D}{C A} $
$ C A^{2}=C B \times C D $
Hence Proved.

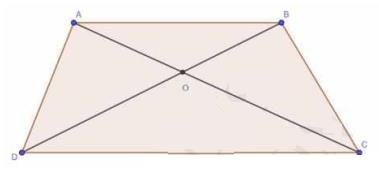
14. Sides $ A B $ and $ A C $ and median $ A D $ of a triangle $ A B C $ are respectively proportional to sides PQ and PR and median PM of another triangle $ P Q R $.
Show that $ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $

Answer

To Prove: $ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $
Given:
$ \frac{A B}{P Q}=\frac{A C}{P R}=\frac{A D}{P M} $
Proof

Let us extend AD and PM up to point E and L respectively, such that $ \mathrm{AD}=\mathrm{DE} $ and $ \mathrm{PM}=\mathrm{ML} $.
Then, join B to E, C to
E, Q to L , and R to L
We know that medians divide opposite sides.
Hence, $ \mathrm{BD}=\mathrm{DC} $ and $ \mathrm{QM}=\mathrm{MR} $
Also, $ \mathrm{AD}=\mathrm{DE} $ (By construction)
And, $ \mathrm{PM}=\mathrm{ML} $ (By construction)
In quadrilateral ABEC,
Diagonals AE and BC bisect each other at point D .
Therefore,
Quadrilateral $ A B E C $ is a parallelogram.
$ \mathrm{AC}=\mathrm{BE} $ and $ \mathrm{AB}=\mathrm{EC} $ (Opposite sides of a parallelogram are equal)
Similarly, we can prove that quadrilateral PQLR is a parallelogram and $ \mathrm{PR}=\mathrm{QL}, \mathrm{PQ}=\mathrm{LR} $
It was given in the question that,
$\frac{A B}{P Q}=\frac{A C}{P R}=\frac{A D}{P M}$
$\frac{A B}{P Q}=\frac{B E}{Q L}=\frac{2 A D}{2 P M}$
$\frac{A B}{P Q}=\frac{B E}{Q L}=\frac{A R}{P L} $
$ \triangle \mathrm{ABE} \sim \triangle \mathrm{PQL}( $ By SSS similarity criterion)
We know that corresponding angles of similar triangles are equal.
$ \angle \mathrm{BAE}=\angle \mathrm{QPL} \quad\ldots \text{(i)}$
Similarly, it can be proved that
$ \triangle \mathrm{AEC} \sim \triangle \mathrm{PLR} $ and $ \angle \mathrm{CAE}=\angle \mathrm{RPL}\quad\ldots \text{(ii)} $
Adding equation (i) and (ii), we obtain
$\angle \mathrm{BAE}+\angle \mathrm{CAE}=\angle \mathrm{QPL}+\angle \mathrm{RPL}$
$\Rightarrow \angle \mathrm{CAB}=\angle \mathrm{RPQ} \quad\ldots \text{(iii)}$
In $ \triangle \mathrm{ABC} $ and $ \triangle \mathrm{PQR} $,
$ \frac{A B}{P Q}=\frac{A C}{P R} \ ( $Given$ ) $
$ \angle \mathrm{CAB}=\angle \mathrm{RPQ}\ [ $Using equation (iii)]
$ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $ (By SAS similarity criterion)
Hence, Proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower

Answer

Let AB and CD be a tower and a pole respectively
And, the shadow of BE and DF be the shadow of AB and CD respectively.

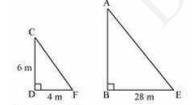
To find: $ A B $
At the same time, the light rays from the sun will fall on the tower and the pole at the same angle
Therefore,
$ \angle \mathrm{DCF}=\angle \mathrm{BAE} $
And,
$ \angle \mathrm{DFC}=\angle \mathrm{BEA} $
$ \angle \mathrm{CDF}=\angle \mathrm{ABE} $ (Tower and pole are vertical to the ground)
$ \triangle \mathrm{ABE} \sim \triangle \mathrm{CDF} $ (AAA similarity)
Hence, By the properties of similar triangles that if two triangles are similar, their corresponding sides will be proportional.
$\frac{A B}{C D}=\frac{B F}{D F}$
$\frac{A B}{6}=\frac{28}{4}$
$\mathrm{AB}=42 \mathrm{~m} $
Height of the Tower $ =42 \mathrm{~m} $

16. If $ A D $ and $ P M $ are medians of triangles $ A B C $ and $ P Q R $, respectively where $ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $, prove that $ \frac{A B}{P Q}=\frac{A D}{P M} $

Answer

It is given that $ \triangle \mathrm{ABC} $ is similar to $ \triangle \mathrm{PQR} $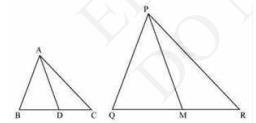

To Prove: $ \frac{A B}{P Q}=\frac{A D}{P M} $
Given: $ \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR} $
AD and PM are medians
We know that the corresponding sides of similar triangles are in proportion
$ \frac{A B}{P Q}=\frac{A C}{P R}=\frac{B C}{Q R} \quad\ldots$ (i)
And also the corresponding angles are equal
$ \angle \mathrm{A}=\angle \mathrm{P}$
$\angle \mathrm{B}=\angle \mathrm{Q}$
$\angle \mathrm{C}=\angle \mathrm{R} \quad\ldots \text{(ii)}$
Since AD and PM are medians, they divide their opposite sides in two equal parts
$ B D=\frac{B C}{2} \text { and }$
$Q M=\frac{Q R}{2} \quad\ldots \text{(iii)}$
From (i) and (iii), we get
$ \frac{A B}{P Q}=\frac{B D}{Q M} \quad\ldots \text{(iv)}$
In $ \triangle \mathrm{ABD} $ and $ \triangle \mathrm{PQM} $,
$ \angle \mathrm{B}=\angle \mathrm{Q}\quad[\operatorname{Using}(\mathrm{ii})] $
$ \frac{A B}{P Q}=\frac{B D}{Q M} \quad[\operatorname{Using}(\mathrm{iv})]$
$ \triangle \mathrm{ABD}\sim \triangle \mathrm{PQM} $ (Since two sides are proportional and one angle is equal then by SAS similarity)
$ \frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M} $
Hence, Proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now