CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

NCERT Class 10 Mathematics Chapter 6: Triangle – For Free. || Get the complete NCERT Solutions for Class 10 Maths Chapter 6: Triangle, covering Exercise 6.6. This free resource helps you understand key concepts and solve problems with ease, perfect for Class 10 students preparing for exams using NCERT Maths materials. We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangle Exercise 6.6 help you. If you have any queries regarding NCERT Maths Solutions Chapter 6 Triangle Exercise 6.6, drop a comment below, and we will get back to you at the earliest.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)
Exercise - 6.6

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

1. In Fig. 6.56, PS is the bisector of $ \angle Q P R $ of $ \triangle P Q R $. Prove that $ \frac{Q S}{S R}=\frac{P Q}{P R} $

Answer

Construct a line segment RT parallel to SP which intersects the extended line segment QP at point T

Given: PS is the angle bisector of $ \angle \mathrm{QPR} $.
Proof:
$ \angle \mathrm{QPS}=\angle \mathrm{SPR} $ (i)
By construction,
$ \angle \mathrm{SPR}=\angle \mathrm{PRT} $ (As $PS || TR$, By interior alternate angles) (ii)
$ \angle \mathrm{QPS}=\angle \mathrm{QTR} $ (As $ PS\| \mathrm{TR} $, By interior alternate angles) (iii)
Using these equations, we get:
$ \angle \mathrm{PRT}=\angle \mathrm{QTR}$
$\mathrm{PT}=\mathrm{PR} $
By construction, $ \mathrm{PS} \| \mathrm{TR} $
Basic Proportionality Theorem: If a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.
By using basic proportionality theorem for $ \triangle Q T R $,
$ \frac{Q S}{S R}=\frac{P Q}{P R} $
Hence, Proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

2. In Fig. 6.57, D is a point on hypotenuse AC of $ \triangle \mathrm{ABC} $, $ \mathrm{DM} \perp \mathrm{BC} $ and $ \mathrm{DN} \perp \mathrm{AB} $. Prove that:
(i) $ \mathrm{DM}^{2}= DN.MC$
(ii) $ \mathrm{DN}^{2}= DM.AN$

Answer

(i) To Prove: $ \mathrm{DM}^{2}=\mathrm{DN} .
\mathrm{MC} $
Construction: join DB
We have, $ \mathrm{DN} \| \mathrm{CB} $,
$ \mathrm{DM} \| \mathrm{AB} $
And $ \angle \mathrm{B}=90^{\circ} $ (Given)
As opposite sides are parallel and equal and also each angle is $ 90^{\circ} $, DMBN is a rectangle.

$ \mathrm{DN}=\mathrm{MB} $ and $ \mathrm{DM}=\mathrm{NB} $
The condition to be proved is the case when $ D $ is the foot of the perpendicular drawn from B to AC
$ \angle \mathrm{CDB}=90^{\circ} $
Now from the figure we can say that
$ \angle 2+\angle 3=90^{\circ}\quad\ldots \text{(i)} $
In $ \triangle \mathrm{CDM} $,
$ \angle 1+\angle 2+\angle D M C=180^{\circ} \quad $ [Sum of angles of a triangle $ =180^{\circ} $ ]
$ \angle 1+\angle 2=90^{\circ} \quad\ldots \text{(ii)}$
In $ \triangle \mathrm{DMB} $,
$ \angle 3+\angle \mathrm{DMB}+\angle 4=180^{\circ} \quad \text { [Sum of angles of a triangle }=$$\mathrm{1 8 0}^{\circ} \text {] }$
$\Rightarrow \angle 3+\angle 4=90^{\circ}\quad\ldots \text{(iii)} $
From (i) and (ii), we get
$ \angle 1=\angle 3 $
From (i) and (iii), we get
$ \angle 2=\angle 4 $
In $ \triangle \mathrm{DCM} $ and $ \triangle \mathrm{BDM} $,
$ \angle 1=\angle 3 $ (Proved above)
$ \angle 2=\angle 4 $ (Proved above)
$ \triangle \mathrm{DCM} $ similar to $ \triangle \mathrm{BDM} $ (AA similarity)
(AA Similarity : When you have two triangles where one is a smaller version of the other, you are looking at two similar triangles.)
$ \frac{\mathrm{BM} }{ \mathrm{DM}}=\frac{\mathrm{DM} }{ \mathrm{MC}} $
Cross multiplying we get,
$ \frac{\mathrm{DN} }{ \mathrm{DM}}=\frac{\mathrm{DM} }{ \mathrm{MC}}(\mathrm{BM}=\mathrm{DN}) $
$ \mathrm{DM}^{2}=\mathrm{DN} \times \mathrm{MC} $
Hence, Proved.
To Prove: $ \mathrm{DN}^{2}=\mathrm{AN} \times \mathrm{DM} $
In right triangle DBN ,
$ \angle 5+\angle 7=90^{\circ} \text { (iv) } $
In right triangle DAN,
$ \angle 6+\angle 8=90^{\circ}(\mathrm{v}) $
$ D $ is the foot of the perpendicular drawn from $ B $ to $ A C $
$ \angle \mathrm{ADB}=90^{\circ} $
$ \angle 5+\angle 6=90^{\circ}(\mathrm{vi}) $
From equation (iv) and (vi), we obtain
$ \angle 6=\angle 7 $
From equation (v) and (vi), we obtain
$ \angle 8=\angle 5 $
In $ \triangle \mathrm{DNA} $ and $ \triangle \mathrm{BND} $,
$ \angle 6=\angle 7 $ (Proved above)
$ \angle 8=\angle 5 $ (Proved above)
Hence,
$ \triangle \mathrm{DNA} $ similar to $ \triangle \mathrm{BND} $ (AA similarity criterion)
(AA similarity Criterion: When you have two triangles where one is a smaller version of the other, you are looking at two similar triangles.)
$ \frac{\mathrm{AN} }{ \mathrm{DN}}=\frac{\mathrm{DN} }{ \mathrm{NB}}$
$\mathrm{DN}^{2}=\mathrm{AN} \times \mathrm{NB} $
$ \mathrm{DN}^{2}=\mathrm{AN} \times \mathrm{DM}(\text{As } \mathrm{NB}=\mathrm{DM}) $
Hence, Proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

$Mathninja.in$

3. In Fig. 6.58, ABC is a triangle in which $ \angle \mathrm{ABC} > 90^{\circ} $ and $ \mathrm{AD} \perp $ CB produced. Prove that $ \mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}+2 \mathrm{~BC} . \mathrm{BD} $.

Answer

Using Pythagoras theorem in $ \triangle \mathrm{ADB} $, we get:
$ \mathrm{AB}^{2}=\mathrm{AD}^{2}+\mathrm{DB}^{2}(\mathrm{i}) $
Applying Pythagoras theorem in $ \triangle \mathrm{ACD} $, we obtain
$ \mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{DC}^{2} $
$ \mathrm{AC}^{2}=\mathrm{AD}^{2}+(\mathrm{DB}+\mathrm{BC})^{2} $
$ \mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{DB}^{2}+\mathrm{BC}^{2}+2 \mathrm{DB} \times \mathrm{BC} $
$ \mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}+2 \mathrm{DB} \times \mathrm{BC} $ [Using equation (i)]

4. In Fig. 6.59, ABC is a triangle in which $ \angle \mathrm{ABC} < 90^{\circ} $ and $ \mathrm{AD} \perp $ $ B C $. Prove that $ A C^{2}=A B^{2}+B C^{2}+2 B C . B D $.

Answer

To Prove: $ A C^{2}=A B^{2}+\mathrm{BC}^{2}-2 B C \times B D $
Given: AD is Perpendicular on BC and angle $ \mathrm{ABC} < 90^{\circ} $
Proof:
Pythagoras Theorem: It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Applying Pythagoras theorem in $ \triangle \mathrm{ADB} $, we obtain
$ \mathrm{AD}^{2}+\mathrm{DB}^{2}=\mathrm{AB}^{2}$
$\mathrm{AD}^{2}=\mathrm{AB}^{2}-\mathrm{DB}^{2} \quad\ldots \text{(i)}$
Applying Pythagoras theorem in $ \triangle \mathrm{ADC} $, we obtain
$ \mathrm{AD}^{2}+\mathrm{DC}^{2}=\mathrm{AC}^{2}$
$\mathrm{AB}^{2}-\mathrm{BD}^{2}+\mathrm{DC}^{2}=\mathrm{AC}^{2} \quad[\text {Using equation (i)}]$
$\mathrm{AB}^{2}-\mathrm{BD}^{2}+(\mathrm{BC}-\mathrm{BD})^{2}=\mathrm{AC}^{2} \quad[\mathrm{DC}=\mathrm{BC}-\mathrm{BD}]$
$\mathrm{AC}^{2}=\mathrm{AB}^{2}-\mathrm{BD}^{2}+\mathrm{BC}^{2}+\mathrm{BD}^{2}-2 \mathrm{BC} \times \mathrm{BD}$
$\mathrm{A C}^{\mathrm{2}}=\mathrm{A B}^{2}+\mathrm{B C}^{2}-\mathrm{2} \mathrm{B C} \times \mathrm{B D} $
Hence, Proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

(i) In Fig. 6.60, AD is a median of a triangle ABC and $ \mathrm{AM} \perp \mathrm{BC} $. Prove that:

$A C^{2}=A D^{2}+B C \cdot D M+\left(\frac{B C}{2}\right)^{2}$

Answer

Using, Pythagoras theorem in $ \triangle \mathrm{AMD} $, we get
$ \mathrm{AM}^{2}+\mathrm{MD}^{2}=\mathrm{AD}^{2} $ (i)
Applying Pythagoras theorem in $ \triangle \mathrm{AMC} $, we obtain
$ \mathrm{AM}^{2}+\mathrm{MC}^{2}=A C^{2}$
$A M^{2}+(M D+D C)^{2}=A C^{2}$
$\left(A M^{2}+\mathrm{MD}^{2}\right)+\mathrm{DC}^{2}+2 \mathrm{MD}^{2} \cdot \mathrm{DC}=\mathrm{AC}^{2}$
$\mathrm{AD}^{2}+\mathrm{DC}^{2}+2 \mathrm{MD} \cdot \mathrm{DC}=\mathrm{AC}^{2}[\text {Using equation (i)}] $
Using, $ \mathrm{DC}=\frac{ \mathrm{BC} }{ 2 } $ we get
$\mathrm{AD}^{2}+(\frac{ \mathrm{BC} }{ 2 })^{2}+2 \mathrm{MD} \times (\frac{ \mathrm{BC} }{ 2 })=\mathrm{AC}^{2}$
$\mathrm{AD}^{2}+(\frac{ \mathrm{BC} }{ 2 })^{2}+\mathrm{MD} \times \mathrm{BC}=\mathrm{AC}^{2} $

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

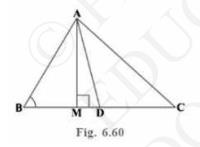
(ii) In Fig. 6.60, AD is a median of a triangle ABC and $ \mathrm{AM} \perp \mathrm{BC} $. Prove that:

$A B^{2}=A D^{2}+B C \cdot D M+\left(\frac{B C}{2}\right)^{2}$

Answer

Using Pythagoras theorem in $ \triangle \mathrm{ABM} $, we obtain
$ A B^{2}=A M^{2}+M B^{2}$
$=\left(A D^{2}-DM^{2}\right)+M B^{2}$
$=\left(\mathrm{AD}^{2}-\mathrm{DM}^{2}\right)+(B D-M D)^{2}$
$=\mathrm{AD}^{2}-\mathrm{DM}^{2}+\mathrm{BD}^{2}+\mathrm{MD}^{2}-2 \mathrm{BD} \times \mathrm{MD}$
$=\mathrm{AD}^{2}+\mathrm{BD}^{2}-2 \mathrm{BD} \times \mathrm{MD}$
$=\mathrm{AD}^{2}+(\frac{ \mathrm{BC} }{ 2 })^{2}-2(\frac{ \mathrm{BC} }{ 2 }) \times \mathrm{MD}$
$=\mathrm{AD}^{2}+(\frac{ \mathrm{BC} }{ 2 })^{2}-\mathrm{BC} \times \mathrm{MD} $

(iii) In Fig. 6.60, AD is a median of a triangle ABC and $ \mathrm{AM} \perp \mathrm{BC} $. Prove that:

$A C^{2}+A B^{2}=2 A D^{2}+\frac{1}{2} B C^{2}$

Answer

Using Pythagoras theorem in $ \triangle \mathrm{ABM} $, we obtain
$ \mathrm{AM}^{2}+\mathrm{MB}^{2}=\mathrm{AB}^{2}(1) $
Applying Pythagoras theorem in $ \triangle \mathrm{AMC} $, we obtain
$ \mathrm{AM}^{2}+\mathrm{MC}^{2}=\mathrm{AC}^{2}(2) $
Adding equations (1) and (2), we obtain
$ 2 \mathrm{AM}^{2}+\mathrm{MB}^{2}+\mathrm{MC}^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2}$
$2 \mathrm{AM}^{2}+(\mathrm{BD}-\mathrm{DM})^{2}+(\mathrm{MD}+\mathrm{DC})^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2}$
$2 \mathrm{AM}^{2}+\mathrm{BD}^{2}+\mathrm{DM}^{2}-2 \mathrm{BD} \cdot \mathrm{DM}+\mathrm{MD}^{2}+\mathrm{DC}^{2}+2 M D \cdot D C$$=\mathrm{AB}^{2}+ \mathrm{AC}^{2}$
$2 \mathrm{AM}^{2}+2 \mathrm{MD}^{2}+\mathrm{BD}^{2}+\mathrm{DC}^{2}+2 \mathrm{MD}(-\mathrm{BD}+\mathrm{DC})=\mathrm{AB}^{2}+\mathrm{AC}^{2}$
$2\left(\mathrm{AM}^{2}+\mathrm{MD}^{2}\right)+(\frac{ \mathrm{BC} }{ 2 })^{2} +(\frac{ \mathrm{BC} }{ 2 })^{2}+2 \mathrm{MD}(-\frac{ \mathrm{BC} }{ 2 }+\frac{ \mathrm{BC} }{ 2 })=\mathrm{AB}^{2}+$
$\mathrm{AC}^{2}$
$2 \mathrm{AD}^{2}+\frac{ \mathrm{BC}^{2} }{ 2 }=\mathrm{AB}^{2}+\mathrm{AC}^{2} $

6. Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides

Answer

$ A B C D $ is a parallelogram in which $ A B=C D $ and $ A D=B C $
Perpendicular AN is drawn on DC and perpendicular DM is drawn on AB extend up to M

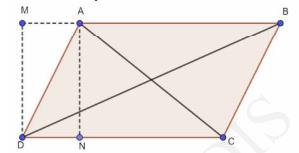
In $ \triangle $ AMD,
$ \mathrm{AD}^{2}=\mathrm{DM}^{2}+\mathrm{AM}^{2} \quad\ldots \text{(i)}$
In $ \triangle BMD$,
$ \mathrm{BD}^{2}=\mathrm{DM}^{2}+(\mathrm{AM}+\mathrm{AB})^{2} $
Or, $ (\mathrm{AM}+\mathrm{AB})^{2}=\mathrm{AM}^{2}+\mathrm{AB}^{2}+2 \mathrm{AM} \times \mathrm{AB} $
$ \mathrm{BD}^{2}=\mathrm{DM}^{2}+\mathrm{AM}^{2}+\mathrm{AB}^{2}+2 \mathrm{AM} \times \mathrm{AB} \quad\ldots \text{(ii)}$
Substituting the value of $ \mathrm{AM}^{2} $ from (i) in (ii), we get
$ \mathrm{BD}^{2}=\mathrm{AD}^{2}+\mathrm{AB}^{2}+2 \times \mathrm{AM} \times \mathrm{AB} \quad\ldots \text{(iii)}$
In $ \triangle AND$,
$ \mathrm{AD}^{2}=\mathrm{AN}^{2}+\mathrm{DN}^{2}\quad\ldots \text{(iv)} $
In $ \triangle \mathrm{ANC} $,
$ \mathrm{AC}^{2}=\mathrm{AN}^{2}+(\mathrm{DC}-\mathrm{DN})^{2} $
Or,
$ \mathrm{AC}^{2}=\mathrm{AN}^{2}+\mathrm{DN}^{2}+\mathrm{DC}^{2}-2 \times \mathrm{DC} \times \mathrm{DN} \quad\ldots \text{(v)}$ Substituting the value of $ \mathrm{AD}^{2} $ from (iv) in (v), we get
$ \mathrm{AC}^{2}=\mathrm{AD}^{2}+\mathrm{DC}^{2}-2 \times \mathrm{DC} \times \mathrm{DN} \quad\ldots \text{(vi)}$
We also have,
$ \mathrm{AM}=\mathrm{DN} $ and $ \mathrm{AB}=\mathrm{CD} $
Substituting these values in (vi), we get
$ A C^{2}=A D^{2}+\mathrm{DC}^{2}-2 \times \mathrm{AM} \times \mathrm{AB} \quad\ldots \text{(vii)}$
Adding (iii) and (vii), we get
$ \mathrm{AC}^{2}+\mathrm{BD}^{2}=\mathrm{AD}^{2}+\mathrm{AB}^{2}+2 \times \mathrm{AM} \times \mathrm{AB}+\mathrm{AD}^{2}+\mathrm{DC}^{2}-$$2 \times \mathrm{AM} \times AB $
Or, $ \mathrm{AC}^{2}+\mathrm{BD}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}+\mathrm{DC}^{2}+\mathrm{AD}^{2} $
Hence, proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

(i) In Fig. 6.61, two chords AB and CD intersect each other at the point P. Prove that:
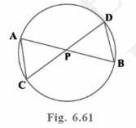
$ \triangle \mathrm{APC} \sim \triangle \mathrm{DPB} $

Answer

In triangle APC and DPB,
$ \angle \mathrm{CAP}=\angle \mathrm{BDP} $ (Angles on the same side of a chord are equal)
$ \angle \mathrm{APC}=\angle \mathrm{DPB} $ (Opposite angles)
Hence,
$ \triangle \mathrm{APC} \sim \triangle \mathrm{DPB} $ (By AAA similarity)

(ii) In Fig. 6.61, two chords AB and CD intersect each other at the point P. Prove that:
$ \mathrm{AP} . \mathrm{PB}=\mathrm{CP} . \mathrm{DP} $

Answer

Since, the two triangles are similar
Hence,
$ \frac{A P}{C P}=\frac{D P}{P B}$
$\text {or } A P \times P B=C P \times D P $
Hence, proved.

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

Q. 8

(i) In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
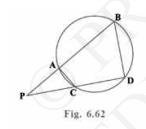
$ \triangle \mathrm{PAC} \sim \triangle \mathrm{PDB} $

Answer

In triangle PAC and PDB
$ \angle \mathrm{PAC}+\angle \mathrm{CAB}=180^{\circ} $ (Linear pair)
$ \angle \mathrm{CAB}+\angle \mathrm{BDC}=180^{\circ} $
(Opposite angles of a cyclic quadrilateral are supplementary)
Hence,
$ \angle \mathrm{PAC}=\angle \mathrm{PDB} $
Similarly, $ \angle \mathrm{PCA}=\angle \mathrm{PBD} $
Hence,
$ \triangle \mathrm{PAC} \sim \triangle \mathrm{PDB} $

(ii) In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
$ \mathrm{PA} \cdot \mathrm{PB}=\mathrm{PC} \cdot \mathrm{PD} $

Answer

Since the two triangles are similar, so
$ \frac{P A}{P C}=\frac{P D}{P B} $
or $ P A \times P B=P C \times P D $
Hence, proved.

9. In Fig. 6.63, $ D $ is a point on side $ B C $ of $ \triangle \mathrm{ABC} $ such that $ \frac{B D}{C D}=\frac{A B}{A C} $ Prove that $ A D $ is the bisector of $ \angle B A C $

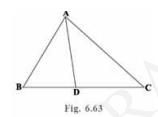
Answer

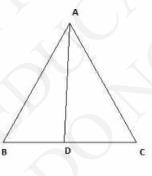
To Prove: AD bisects $ \angle \mathrm{BAC} $ Given: $ \frac{B C}{C D}=\frac{A B}{A C} $
Now from $ \triangle \mathrm{ABD} $ and $ \triangle \mathrm{ADC} $, As it is given that $ \frac{B C}{C D}=\frac{A B}{A C} $
And, AD is common to both triangles, Therefore, $ \triangle \mathrm{ABD} \sim \triangle \mathrm{ADC} $ (BY SSS theorem)Now by similarity $ \angle B A D=\angle D A C $ Hence, $ A D $ must be the bisector of the angle BAC.

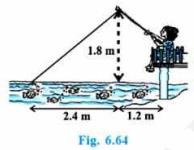
10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string(from the tip of her rod to the fly) is taut, how much string does she have out(see Fig. 6.64)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Answer

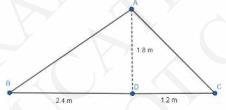
As per the question:
$ \mathrm{AD}=1.8 \mathrm{~m}$
$\mathrm{BD}=2.4 \mathrm{~m}$
$\mathrm{CD}=1.2 \mathrm{~m} $
speed of string when she pulls in $ =5 \mathrm{~cm} $ per second
To find: Length of string, $ A B $ and
In triangle $ A B D $, length of string i.e. $ A B $ can be calculated as follows [By Pythagoras theorem]
$ \mathrm{AB}^{2}=\mathrm{AD}^{2}+\mathrm{BD}^{2} $
$ =(1.8)^{2}+(2.4)^{2}$
$=3.24+5.76$
$=9 $
Or, $ \mathrm{AB}=3 \mathrm{~m} $

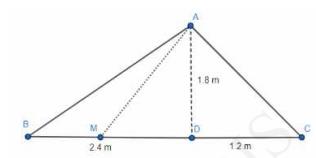
Let us assume that the string reaches at point M after 12 seconds
Now, To find: Distance of fly, from the girl.
Length of string pulled in, after 1 second $ =5 \mathrm{~cm} $
Length of string pulled in, after 12 seconds $ =5 \times 12=60 \mathrm{~cm} $
$ =0.6 \mathrm{~m} \quad[\text { As, } 1 \mathrm{~m}=100 \mathrm{~cm}] $
Remaining length, $ \mathrm{AM}=3-0.6=2.4 \mathrm{~m} $
In triangle AMD, we can find MD by using Pythagoras theorem,
$\mathrm{MD}^{2} =\mathrm{AM}^{2}-\mathrm{AD}^{2}$
$ =2.4^{2}-1.8^{2}$
$ =5.76-3.24$
$ =2.52 \mathrm{~m} $
Or, $ \mathrm{MD}=1.58 \mathrm{~m} $
Also,
Horizontal distance between the girl and the fly = $CD + MD =1.2+1.58=2.78 \mathrm{~m} $

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now

CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6 || NCERT Solutions for Class 10 Maths Chapter 6: Triangle(English Medium)

Download the Math Ninja App Now