CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3 || NCERT Solutions for Class 10 Maths Chapter 7: Coordinate Geometry(English Medium)

Let the vertices of the triangle be \( \mathrm{A}(0,-1), \mathrm{B}(2,1), \mathrm{C}(0 \), 3)
We know, mid-points of a line joining points \( \left(y_{1}, y_{1}\right) \) and \( \left(x_{2}, y_{2}\right) \) is given by
\( \left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right) \)
Let \( \mathrm{D}, \mathrm{E}, \mathrm{F} \) be the mid-points of the sides of this triangle. Coordinates of \( \mathrm{D}, \mathrm{E} \), and F are given by

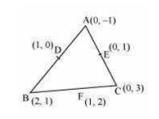
\( D=\left(\frac{0+2}{2}, \frac{-1+1}{2}\right)=(1,0) \)
\( E=\left(\frac{0+0}{2}, \frac{3-1}{2}\right)=(0,1)\)
\(F=\left(\frac{2+0}{2}, \frac{1+3}{2}\right)=(1,2) \)
Also, we know area of a triangle having \( \left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right) \) and \( \left(x_{3}, y_{3}\right) \) is
\( \frac{1}{2}\left(x_{1}\left(y_{2}-y_{3}\right)+x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right) \)
Area of the triangle \( (\mathrm{DEF})=\frac{1}{2}[1(2-1)+1(1-0)+0(0-2) \)
\( =\frac{1}{2}(1+1) \)
\( =1 \) square unit
Area of the triangle \( (\mathrm{ABC})=^{\frac{1}{2}}[0(1-3)+2(3+1)+0(-1-1) \)
\( =\frac{1}{2} \times 8 \)
\( =4 \) square units
Therefore, required ratio \( =1: 4 \).

Let the vertices of the quadrilateral be \( \mathrm{A}(-4,-2) \), B ( - 3, \( 5), C(3,-2) \), and \( D(2,3) \). Join \( A C \) to form two triangles \( \triangle A B C \) and \( \triangle \mathrm{ACD} \)

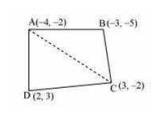
Area of the triangle \( (\mathrm{ABC})=\frac{1}{2}[-4(-5+2)-3(-2+2)+3(-2+5)] \) \( =\frac{1}{2}(12+0+9) \)
\( =\frac{21}{2} \) Square units
Area of the triangle \( (\mathrm{ACD})=\frac{1}{2}[-4(-2-3)+3(3+2)+2(-2+2)] \)
\( =\frac{1}{2}(20+15+0) \)
\( =\frac{35}{2} \) Square units
Area of Quadrilateral \( \mathrm{ABCD}= \) Area of the triangle \( (\mathrm{ABC})+ \) Area of the triangle \( (\mathrm{ACD}) \)
\( =\frac{21}{2}+\frac{35}{2} \)
\( =\frac{56}{2} \)
\( =28 \) Square units

Let the vertices of the triangle be A \( (4,-6), B(3,-2) \), and C \( (5,2) \)
Let D be the mid-point of side BC of \( \triangle \mathrm{ABC} \)
Therefore, AD is the median in \( \triangle \mathrm{ABC} \)
To prove: Area \( \triangle \mathrm{ABC}= \) Area \( \triangle \mathrm{ABD}+ \) Area \( \triangle \mathrm{ADC} \)

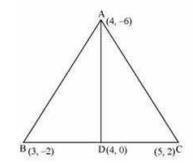
Midpoint of the line joining the points \( A\left(x_{1}, y_{1}\right) \) and \( B\left(x_{2}, y_{2}\right) \) is given by
\( X=\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2} \)
Therefore, by applying the formula we can get the coordinate of D Coordinate of point \( D=\left(\frac{3+5}{2}, \frac{-2+2}{0}\right)=(4,0) \)
We also know that if \( \mathrm{A}\left(x_{1}, y_{1}\right), \mathrm{B}\left(x_{2}, y_{2}\right) \) and \( \mathrm{C}\left(x_{3}, y_{3}\right) \) are vertices of a triangle then
Area of triangle is given by,
\( \text { Area }=\frac{1}{2}\left[x_{1}\left(y_{2}-y_{3}\right)-x_{2}\left(y_{3}-y_{1}\right)+x_{3}\left(y_{1}-y_{2}\right)\right] \)
For \( A(4,-6), B(3,-2) \), and \( C(5,2) \)
Area of the \( \Delta(\mathrm{ABC})=\frac{1}{2}[4(-2-2)+3(0+8)+5(-6+2)] \)
\( =\frac{1}{2}(-8+32-30) \)
\( =-3 \) Square units
However, area cannot be negative. Therefore, area of \( \triangle \mathrm{ADC} \) is 3 square units
Now for for \( A(4,-6), B(3,-2) \) and \( D(4,0) \) Area of \( \Delta A B D \) \( =\frac{1}{2}[4(-2-0)+3(0+6)+4(-6+2)] \)
Area \( =\frac{1}{2}[-8+18-16] \)
Area \( =-3 \) square units Now the Area cannot be negative so Area of \( \triangle \mathbf{A B D}=3 \) units
Area of \( \triangle \mathrm{ABD}+ \) Area of \( \Delta \mathrm{ADC}=3+3 \) square units
Area of \( \triangle \mathrm{ABD}+ \) Area of \( \Delta \mathrm{ADC}=6= \) Area of \( \triangle \mathrm{ABC} \)
Clearly, median AD has divided \( \triangle \mathrm{ABC} \) in two triangles of equal areas