4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Answer
From the figure:The greatest diameter possible for the hemisphere is equal to the cube's edge \( =7 \mathrm{~cm} \)
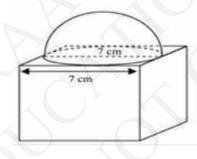
Radius (r) of hemispherical part \( =\frac{ 7 }{ 2 } \mathrm{~cm} \)
The total surface area of solid \(=\) Surface area of cubical part \(+\) CSA of hemispherical part \(-\) Area of the base of hemispherical part
\(=6(\text {Edge})^{2}+2 \pi \mathrm{r}^{2}-\pi \mathrm{r}^{2}\)
\(=6(\text {Edge})^{2}+\pi \mathrm{r}^{2}\)
Total surface area of solid \( =6(7)^{2}+\left(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\right) \)
\(=294+\frac{77}{2}\)
\(=294+38.5\)
\(=332.5 \mathrm{~cm}^{2}\)
5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter 1 of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Answer
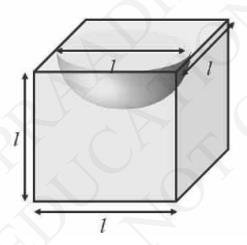
According to the question,
Diameter of hemisphere \( = \) Edge of cube \( =1 \)
Radius of hemisphere \( =\frac{l}{2} \)
Curved Surface Area of hemisphere \( =2 \pi \mathrm{r}^{2} \)
Surface Area of cube \( =6(\text {Edge})^{2} \)
Total surface area of solid \( = \) Surface area of cubical part \(+\) CSA of hemispherical part \(-\) Area of base of hemispherical part
\(=6(\text {Edge})^{2}+2 \pi \mathrm{r}^{2}-\pi \mathrm{r}^{2}\)
\(=6(\text {Edge}) 2+\pi \mathrm{r}^{2}\)
TSA of Solid \( =612+\pi \times\left(\frac{l}{2}\right)^{2} \)
\( =612+\left(\pi \times\left(\frac{l}{2}\right)^{2}\right) \)
\( =612+\left(\frac{l^{2}}{4} \pi\right) \)
\( =12\left(\frac{24+\pi}{4}\right) \) sq. units
NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.1
Download the Math Ninja App Now6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig. 13.10). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
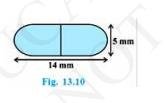

Answer
According to the question,Radius (r) of cylindrical part \( = \) Radius \( (\mathrm{r}) \) of hemispherical part
\(=\frac{\text {di ameter of the capsule}}{2}\)
\(=\frac{5}{2}\)
Length of cylindrical part \( (\mathrm{h})= \) Length of the entire capsule \( -2 \times \mathrm{r} \)
\(=14-5=9 \mathrm{~cm}\)
Surface area of capsule \( =2 \times \) CSA of hemispherical part \(+\) CSA of cylindrical part
(Curved Surface Area of cylinder \( =2 \pi \mathrm{rh} \), Curved Surface Area of Hemisphere \( =2 \pi r^{2} \))
\(=2 \times 2 \pi \mathrm{r}^{2}+2 \pi \mathrm{rh}\)
\(=4 \pi\left(\frac{5}{2}\right)^{2}+2 \pi \frac{5}{2} \times 9\)
\(=25 \pi+45 \pi\)
\(=70 \pi\)
7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per \( \mathrm{m}^{2} \). (Note that the base of the tent will not be covered with canvas)
Answer
Given:Height (h) of the cylindrical part \( =2.1 \mathrm{~m} \)
Diameter of the cylindrical part \( =4 \mathrm{~m} \)
Radius of the cylindrical part \( =2 \mathrm{~m} \)
Slant height \( (1)=2.8 \mathrm{~m} \)
Solution:
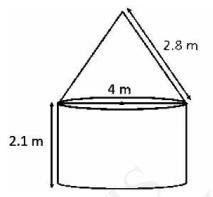
We know for a cone,
Area of canvas used \( = \) CSA of conical part \(+\) CSA of cylindrical part \( =\pi \mathrm{r}^{1}+2 \pi \mathrm{rh} \)
\( =(\pi \times 2 \times 2.8)+(2 \pi \times 2 \times 2.1) \)
\( =2 \pi[2.8+(2 \times 2.1)] \)
\( =2 \pi[2.8+4.2] \)
\( =2 \times \frac{22}{7} \times 7 \)
\( =44 \mathrm{~m}^{2} \)
Cost of \( 1 \mathrm{~m}^{2} \) canvas \( = \) Rs 500
Cost of \( 44 \mathrm{~m}^{2} \) canvas \( =44 \times 500= \) Rs 22000
NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.1
Download the Math Ninja App Now8. From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest \( \mathrm{cm}^{2} \).
Answer
Given: 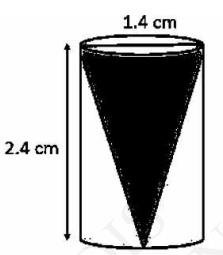
Height \( (\mathrm{h}) \) of the conical part \( = \) Height \( (\mathrm{h}) \) of the cylindrical part \( =2.4 \) cm
Diameter of the cylindrical part \( =1.4 \mathrm{~cm} \)
Radius (r) of the cylindrical part \( =0.7 \mathrm{~cm} \)
we know, slant height of cone, \( l=\sqrt{r^{2}+h^{2}} \)
Slant height of the cylindrical part
\( (l)=\sqrt{(0.7 \times 0.7)+(2.4 \times 2.4)} \)
\(=\sqrt{0.49+5.76}\)
\(=\sqrt{6.25}\)
\(=2.5\)
Total surface area of the remaining solid will be
\( = \) CSA of cylindrical part \(+\) CSA of conical part \(+\) Area of cylindrical base
\(=2 \pi \mathrm{rh}+\pi \mathrm{r}^{1}+\pi \mathrm{r}^{2}\)
\(=\left(2 \times \frac{22}{7} \times 0.7 \times 2.4\right)+\left(\frac{22}{7} \times 0.7 \times 2.5\right)+\left(\frac{22}{7} \times 0.7 \times 0.7\right)\)
\(=(4.4 \times 2.4)+(2.2 \times 2.5)+(2.2 \times 0.7)\)
\(=10.56+5.50+1.54\)
\(=12.10+5.50 \mathrm{~cm}^{2}\)
\(=17.60 \mathrm{~cm}^{2} (\text {approx.})\)
Hence, the total surface area of remaining solid is \( 17.60 \mathrm{~cm}^{2} \).
NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.1
Download the Math Ninja App Now9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
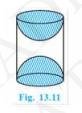

Answer
Given:Radius (r) of cylindrical part \( =3.5 \mathrm{~cm} \)
Radius (r) of hemispherical part \( =3.5 \mathrm{~cm} \)
Height of cylindrical part (h) 10 cm
Surface area of article \( = \) CSA of cylindrical part \( +2 \times \) CSA of hemispherical part \( =2 \pi \mathrm{rh}+2 \times 2 \pi \mathrm{r}^{2} \)
\(=(2 \pi \times 3.5 \times 10)+(2 \times 2 \pi \times 3.5 \times 3.5)\)
\(=70 \pi+49 \pi\)
\(=119 \pi\)
\(=119 \times \frac{22}{7}\)
\( =17 \times 22 \)
\( =374 \mathrm{~cm}^{2} \)
Hence, the total surface of the article \( =374 \mathrm{~cm}^{2} \).
NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.1
Download the Math Ninja App NowCentral Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.3
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.5
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.6
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.1
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.2
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.4
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4
Class 10 : NCERT Solutions for Class 10 Maths Chapter 9
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2