CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Explore the NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry (English Medium), with detailed explanations for Exercise 8.1. This resource is designed to simplify complex Introduction to Trigonometry, helping Class 10 Maths students grasp the subject effortlessly. For any queries regarding NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1, feel free to leave a comment, and we’ll respond as soon as possible. || Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry (English Medium)

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)
Exercise 8.1

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

1. In $ \triangle \mathrm{ABC} $ right angled at $ \mathrm{B}, \mathrm{AB}=24 \mathrm{~cm}, \mathrm{BC}=7 \mathrm{~m} $. Determine
(i) $ \sin A, \cos A $
(ii) $ \sin C, \cos C $

Answer

Applying Pythagoras theorem for $ \triangle A B C $, we obtain
$ A C^{2}=A B^{2}+B C^{2} $
$ =(24 \mathrm{~cm})^{2}+(7 \mathrm{~cm})^{2} $
$=(576+49) \mathrm{cm}^{2}$
$=625 \mathrm{~cm}^{2}$
$\therefore A C=\sqrt{625} \mathrm{~cm}=25 \mathrm{~cm}$

$\sin A=\frac{\text { Side opposite to } \angle A}{\text { Hypotenuse }}=\frac{B C}{A C}$
$=\frac{7}{25}$
$\cos A=\frac{\text { Side adjacent to } \angle A}{\text { Hypotenuse }}=\frac{A B}{A C}=\frac{24}{25}$

(ii) $ \sin C=\frac{\text { Side opposite to } \angle C}{\text { Hypotenuse }}=\frac{A B}{A C} $ $ =\frac{24}{25} $
$ \cos \mathrm{C}=\frac{\text { Side adjacent to } \angle \mathrm{C}}{\text { Hypotenuse }}=\frac{\mathrm{BC}}{\mathrm{AC}} =\frac{7}{25} $

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

2. In the given figure find $ \tan \mathrm{P}-\cot \mathrm{R} $.

Answer

Applying Pythagoras theorem for $ \triangle P Q R $, we obtain
$ P R^{2}=P Q^{2}+Q R^{2} $
$ (13 \mathrm{~cm})^{2}=(12 \mathrm{~cm})^{2}+Q R^{2} $
$169 \mathrm{~cm}^{2}=144 \mathrm{~cm}^{2}+Q R^{2}$
$25 \mathrm{~cm}^{2}=Q R^{2}$
$Q R=5 \mathrm{~cm}$

$\tan \mathbf{P} =\frac{\text { Side opposite to } \angle P}{\text { Side adjacent to } \angle P}=\frac{Q R}{P Q}$
$ =\frac{5}{12}$
$\cot R =\frac{\text { Side adjacent to } \angle R}{\text { Side opposite to } \angle R}=\frac{Q R}{P Q}$
$ =\frac{5}{12}$
$\tan P -\cot \mathrm{R}=\frac{5}{12}-\frac{5}{12}=0$

3. If $ \sin A=\frac{3}{4} $, calculate $ \cos A $ and $ \tan A $.

Answer

Let $ \triangle A B C $ be a right-angled triangle, right-angled at point $ B $

Given that,
$\sin A=\frac{3}{4}$
$\frac{B C}{A C}=\frac{3}{4}$
Let $ B C $ be $ 3 k $. Therefore, $ A C $ will be $ 4 k $, where $ k $ is a positive integer.
Applying Pythagoras theorem in $ \triangle A B C $, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$(4 k)^{2}=A B^{2}+(3 k)^{2}$
$16 k^{2}-9 k^{2}=A B^{2}$
$7 k^{2}=A B^{2}$
$A B=\sqrt{7} k$
$\cos A =\frac{\text { Side adjacent to } \angle A}{\text { Hypotent } t 0 \angle A}$
$ =\frac{A B}{A C}=\frac{\sqrt{7 k}}{4 k}=\frac{\sqrt{7}}{4}$
$\tan A =\frac{\text { Side opposite to } \angle A}{\text { Side adjacent to } \angle \bar{A}}$
$ =\frac{B C}{A B}=\frac{3 k}{\sqrt{7} k}=\frac{3}{\sqrt{7}}$

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

4. Given $ 15 \cot A=8 $. Find $ \sin A $ and $ \sec A $.

Answer

Consider a right-angled triangle, right-angled at B .

Given that,
$\sin A=\frac{3}{4}$
$\frac{B C}{A C}=\frac{3}{4}$
Let $ B C $ be $ 3 k $. Therefore, $ A C $ will be $ 4 k $, where $ k $ is a positive integer.
Applying Pythagoras theorem in $ \triangle \mathrm{ABC} $, we obtain
$\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}$
$(4 k)^{2}=\mathrm{AB}^{2}+(3 \mathrm{k})^{2}$
$16 \mathrm{k}^{2}-\mathrm{gk}^{2}=\mathrm{AB}^{2}$
$7 k^{2}=\mathrm{AB}^{2}$
$\mathrm{AB}=\sqrt{7} k$
$\cos A =\frac{\text { Side adjacent to } \angle A}{\text { Hypotenuse }}$
$ =\frac{A B}{A C}=\frac{\sqrt{7 k}}{4 k}=\frac{\sqrt{7}}{4}$
$\tan A =\frac{\text { Side opposite to } \angle A}{\text { Side adjacent to } \angle A}$
$=\frac{B C}{A B}=\frac{3 k}{\sqrt{7} k}=\frac{3}{\sqrt{7}}$
$\cot A =\frac{\text { Side adjacent to } \angle A}{\text { Side opposite to } \angle A}$
$=\frac{A B}{B C}$
It is given that,
$\cot A=\frac{8}{15}$
$\frac{A B}{B C}=\frac{8}{15}$
Let $ A B $ be $ 8 k $.Therefore, $ 3 C $ will be $ 15 k $, where $ k $ is a positive integer.
Applying Pythagoras theorem in $ \triangle \mathrm{ABC} $, we obtain
$\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}$
$=(8 k)^{2}+(15 k)^{2}$
$=64 k^{2}+225 \mathrm{k}^{2}$
$=289 \mathrm{k}^{2}$
$\mathrm{AC}=17 k$
$\sin A =\frac{\text { Side opposite to } \angle A}{\text { Hypotenuse }}=\frac{B C}{A C}$
$ =\frac{15 k}{17 k}=\frac{15}{17}$
$\sec A =\frac{\text { Hypotenuse }}{\text { Side adjacent to } \angle A}$
$ =\frac{A C}{A B}=\frac{17}{8}$

5. Given $ \sec \theta=\frac{13}{12} $, calculate all other trigonometric ratios.

Answer

Consider a right-angle $ \triangle \mathrm{ABC} $, right-angled at point B

$\sec \theta=\frac{\text { Hypotenuse }}{\text { Side adjacent to } \angle \theta}$
$\frac{13}{12}=\frac{\mathrm{AC}}{\mathrm{AB}}$
If $ A C $ is $ 13 k, A B $ will be $ 12 k $, where $ k $ is a positive integer.
Applying Pythagoras theorem in AABC, we obtain
$(A C)^{2}=(A B)^{2}+(B C)^{2}$
$(13 k)^{2}=(12 k)^{2}+(B C)^{2}$
$169 k^{2}=144 k^{2}+B C^{2}$
$25 k^{2}=B C^{2}$
$BC =5 \mathrm{k}$
$\sin \theta=\frac{\text { Side opposite to } \angle \theta}{\text { Hypotenuse }}=\frac{B C}{A C}=\frac{5 k}{13 k}=\frac{5}{13}$
$\cos \theta=\frac{\text { Side adjacent to } \angle \theta}{\text { Hypotenuse }}=\frac{A B}{A C}=\frac{12 k}{13 k}=\frac{12}{13}$
$\tan \theta=\frac{\text { Side opposite to } \angle \theta}{\text { Side adjacent to } \angle \theta}=\frac{B C}{A B}=\frac{5 k}{12 k}=\frac{5}{12}$
$\cot \theta=\frac{\text { Side adjacent to } \angle \theta}{\text { Side oopposite to } \angle \theta}=\frac{A B}{B C}=\frac{12 k}{5 k}=\frac{12}{5}$
$\operatorname{cosec} \theta=\frac{\text { Hypotenuse }}{\text { Side opposite to } \angle \theta}=\frac{A C}{B C}=\frac{13 k}{5 k}=\frac{13}{5}$

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

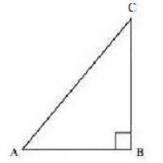
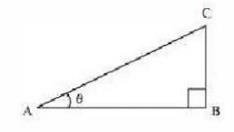
6. If $ \angle A $ and $ \angle B $ are acute angles such that $ \cos A=\cos B $, then show that $ \angle A=\angle B $

Answer

Let us consider a triangle ABC in which $ C D \perp \mathrm{AB} $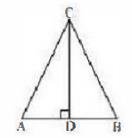

It is given that,
$ \cos A=\cos B $
$ \Rightarrow \frac{A D}{A C}=\frac{B D}{B C} \ldots(1) $
We have to prove $ \angle A=\angle B $. To prove this, let us extend AC to P such that $ \mathrm{BC}=\mathrm{CP} $

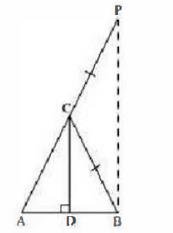
From equation (1) we obtain,
$\frac{A D}{B D}=\frac{A C}{B C}\quad(\text { By construction, we have } B C=C P)$
$\Rightarrow \frac{A D}{B D}=\frac{A C}{C P} \ldots(2)$
By using the converse of B.P.T,
$ \mathrm{CD} \| \mathrm{BP} $
$ \Rightarrow \angle \mathrm{ACD}=\angle \mathrm{CPB} $ ( Corresponding angles ) $ \ldots (3)$
And, $ \angle \mathrm{BCD}=\angle \mathrm{CBP} $ (Alternate interior angles) $ \ldots (4)$
By construction, we have $ \mathrm{BC}=\mathrm{CP} $.
$ \therefore \angle \mathrm{CBP}=\angle \mathrm{CPB} $ (Angle opposite to equal sides of a triangle) $ \ldots (5)$
From equations (3), (4), and (5), we obtain
$\angle \mathrm{ACD}=\angle \mathrm{BCD} \ldots(6)$
$\angle C D A=\angle C D B\left[B o t h 90^{\circ}\right]$
Therefore, the remaining angles should be equal.
$\therefore \angle C A D=\angle C B D$
$\Rightarrow \angle A=\angle B$
Alternatively,
Let us consider triangle ABC in which $ C D \perp A B $

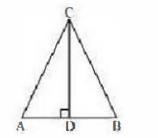
It is given that,
$ \operatorname{Cos} A=\operatorname{Cos} B $
$ \Rightarrow \frac{A D}{A C}=\frac{B D}{B C} $
$ \Rightarrow \frac{A D}{B D}=\frac{A C}{B C} $
Let $ \frac{A D}{B D}=\frac{A C}{B C}=k $
$ \Rightarrow A D=k B D \ldots(1) $
And, $ A C=k B C \ldots(2) $
using Pythagoras theorem for triangles CAD and CBD, we obtain $ \mathrm{CD}^{2}=\mathrm{AC}^{2}-\mathrm{AD}^{2} \ldots(3) $
And, $ \mathrm{CD}^{2}=\mathrm{BC}^{2}-\mathrm{BD}^{2} \ldots $ (4)
From equations (3) and (4), we obtain
$\mathrm{AC}^{2}-\mathrm{AD}^{2}=\mathrm{BC}^{2}-\mathrm{BD}^{2}$
$\Rightarrow(k B C)^{2}-(k B D)^{2}=B C^{2}-B D^{2}$
$\Rightarrow k^{2}\left(B C^{2}-B D^{2}\right)=B C^{2}-B D^{2}$
$\Rightarrow k^{2}=1$
$\Rightarrow k=1$
Putting this value in equation (2), we obtain
$ \mathrm{AC}=\mathrm{BC} $
$ \Rightarrow \angle A=\angle B $ (Angles opposite to equal sides of a angle)

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

7. If $ \cot \theta=\frac{7}{8} $, evaluate
(i) $ \frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)} $
(ii) $ \cot ^{2} \theta $

Answer

Let us consider a right triangle ABC , right-angled at point B .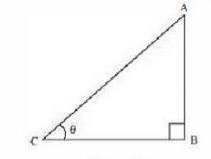

$\cot \theta =\frac{\text { Side adjacent to } \angle \theta}{\text { Side opposite to } \angle \theta}=\frac{\mathrm{BC}}{\mathrm{AB}}$
$ =\frac{7}{8}$
If $ B C $ is $ 7 k $, then $ A B $ will be $ 8 k $, where $ k $ is a positive integer.
Applying Pythagoras theorem in $ \triangle \mathrm{ABC} $, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$=(8 k)^{2}+(7 k)^{2}$
$=64 k^{2}+49 k^{2}$
$=113 k^{2}$
$A C=\sqrt{113} k$
$\sin \theta=\frac{\text { Side opposite to } \angle \theta}{\text { Hypotenuse }}=\frac{\mathrm{AB}}{\mathrm{AC}}$
$=\frac{8 k}{\sqrt{113} k}=\frac{8}{\sqrt{113}}$
$\cos \theta =\frac{\text { Side adjacent to } \angle \theta}{\text { Hypotenuse }}=\frac{\mathrm{BC}}{\mathrm{AC}}$
$= \frac{7 k}{\sqrt{113} k}=\frac{7}{\sqrt{113}} $
(i) $ \frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{\left(1-\sin ^{2} \theta\right)}{\left(1-\cos ^{2} \theta\right)} $
$=\frac{1-\left(\frac{8}{\sqrt{113}}\right)^{2} 1-\frac{64}{113}}{1-\left(\frac{7}{\sqrt{113}}\right)^{2}1-\frac{49}{113}}$
$ =\frac{\frac{49}{113}}{\frac{64}{113}}=\frac{49}{64} $
(ii) $ \cot ^{2} \theta=(\cot \theta)^{2}=\left(\frac{7}{8}\right)^{2}=\frac{49}{64} $

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

$Mathninja.in$

8. If $ 3 \cot A=4 $, Check whether $ \frac{1-\tan ^{2}}{1+\tan ^{2}} \frac{A}{A}=\cos ^{2} A-\sin ^{2} A $ or not.

Answer

It is given that $ 3 \operatorname{Cot} A=4 $
Or, $ \operatorname{Cot} A=\frac{4}{3} $
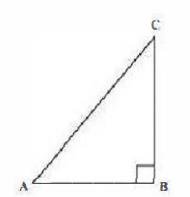
Consider a right triangle ABC , right-angled at point B .

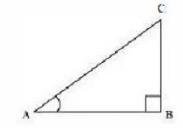
$\cot A=\frac{\text { Side adjacent to } \angle A}{\text { Side opposite to } \angle A}$
$\frac{A B}{B C}=\frac{4}{3}$
If AB is $4 k $, then BC will be $3 k $, where $k$ is a positive integer.
In $ \triangle A B C $,
$(A C)^{2}=(A B)^{2}+(B C)^{2}$
$=(4 k)^{2}+(3 k)^{2}$
$=16 k^{2}+9 k^{2}$
$=25 k^{2}$
$A C=5 k$
$\cos A =\frac{\text { Side adjacent to } \angle A}{\text { Hypotenuse }}=\frac{A B}{A C}$
$ =\frac{4 k}{5 k}=\frac{4}{5}$
$\sin A =\frac{\text { Side opposite to } \angle A}{\text { Hypotenuse }}=\frac{B C}{A C}$
$ =\frac{3 k}{5 k}=\frac{3}{5}$
$\tan A =\frac{\text { Side opposite to } \angle A}{\text { Hypotenuse }}=\frac{B C}{A B}$
$ =\frac{3 k}{4 k}=\frac{3}{4}$
$\frac{1-\tan ^{2} A}{1+\tan ^{2} A}=\frac{1-\left(\frac{3}{4}\right)^{2}}{1+\left(\frac{3}{4}\right)^{2}}=\frac{1-\frac{9}{16}}{1+\frac{9}{16}}$
$=\frac{\frac{7}{16}}{\frac{25}{16}}=\frac{7}{25}$
$\cos ^{2} A-\sin ^{2} A=\left(\frac{4}{5}\right)^{2}-\left(\frac{3}{5}\right)^{2}$
$=\frac{16}{25}-\frac{9}{25}=\frac{7}{25}$
$\therefore \frac{1-\tan ^{2} A}{1+\tan ^{2} A}=\cos ^{2} A-\sin ^{2} A$

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

9. In $ \triangle A B C $, right angled at $ B $. If $ A=\frac{1}{\sqrt{3}} $, find the value of
(i) $ \sin A \cos C+\cos A \sin C $
(ii) $ \cos A \cos C-\sin A \sin C $

Answer

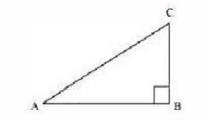
$\tan A=\frac{1}{\sqrt{3}}$
$\frac{B C}{A B}=\frac{1}{\sqrt{3}}$
If $ B C $ is $ k $, then $ A B $ will be, where $ k $ is a positive integer.
In $ \triangle A B C $,
$\mathrm{A} C^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}$
$=(\sqrt{3} k)^{2}+(k)^{2}$
$=3 \mathrm{k}^{2}+\mathrm{k}^{2}=4 \mathrm{k}^{2}$
$\therefore \mathrm{AC}=2 \mathrm{k}$
$\sin A=\frac{\text { Side opposite to } \angle A}{\text { Hypotenuse }}=\frac{B C}{A C}=\frac{k}{2 k}=\frac{1}{2}$
$\cos A=\frac{\text { Side adjacent to } \angle A}{\text { Hypotenuse }}=\frac{A B}{A C}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}$
$\sin C=\frac{\text { Side opposite to } \angle C}{\text { Hypotenuse }}=\frac{A B}{A C}=\frac{\sqrt{3 k}}{2 k}=\frac{\sqrt{3}}{2}$
$\cos C=\frac{\text { Side adjacent to } \angle C}{\text { Hypotenuse }}=\frac{B C}{A C}=\frac{k}{2 k}=\frac{1}{2}$
(i) $ \sin A \cos C+\cos A \sin C $
$=\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)+\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{1}{4}+\frac{3}{4}$
$=\frac{4}{4}=1$
(ii) $ \cos A \cos C-\sin A \sin C $
$=\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)-\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}=0$

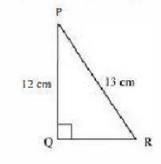
10. In $ \triangle \mathrm{PQR} $, right angled at $ \mathrm{Q}, \mathrm{PR}+\mathrm{QR}=25 \mathrm{~cm} $ and $ \mathrm{PQ}=5 \mathrm{~cm} $. Determine the values of $ \sin P, \cos P $ and $ \tan P $

Answer

Given that, $ \mathrm{PR}+\mathrm{QR}=25 $
$P Q=5$
Let $ P R $ be $ x $.
Therefore, $ \mathrm{QR}=25-x $

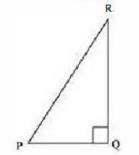
Applying Pythagoras theorem in $ \triangle P Q R $, we obtain
$\mathrm{PR}^{2}=\mathrm{PQ}^{2}+\mathrm{QR}^{2}$
$x^{2}=(5)^{2}+(25-x)^{2}$
$x^{2}=25+625+x^{2}-50 x$
$50 x=650$
$x=13$
Therefore, $ \mathrm{PR}=13 \mathrm{~cm} $
$\mathrm{QR}=(25-13) \mathrm{cm}=12 \mathrm{~cm}$
$\sin \mathrm{P}=\frac{\text { Side opposite to } \angle \mathrm{P}}{\text { Hypotenuse }}=\frac{\mathrm{QR}}{\mathrm{PR}}=\frac{12}{13}$
$\cos P=\frac{\text { Side adjacent to } \angle P}{\text { Hypotenuse }}=\frac{P Q}{P R}=\frac{5}{13}$
$\tan P=\frac{\text { Side opposite to } \angle P}{\text { Side adjacent to } \angle P}=\frac{Q R}{P Q}=\frac{12}{5}$

11.

(i) State whether the following are true or false. Justify your answer.
The value of $ \tan A $ is always less than 1.

Answer

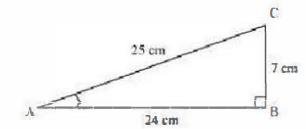
Consider a $ \triangle \mathrm{ABC} $, right-angled at $ B $.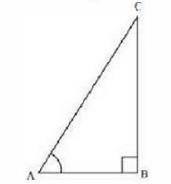

$ \tan A=\frac{\text { Side opposite to } \angle A}{\text { Side adjacent to } \angle A} $
$=\frac{12}{5}$
But $ \frac{12}{5} > 1 $
$ \therefore \tan A > 1 $
So, $ \tan A < 1 $ is not always true.
Hence, the given statement is false.

(ii) State whether the following are true or false. Justify your answer.
$ \sec A=\frac{12}{5} $ for some value of angle A .

Answer

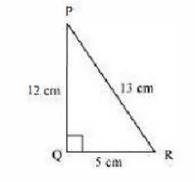
$ \sec A=\frac{12}{5} $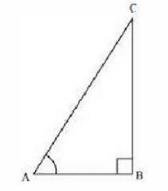

$\frac{\text { Hypotenuse }}{\text { Side adjacent to } \angle A}=\frac{12}{5}$
$\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{12}{5}$
Let $ A C $ be $ 12 k, A B $ will be $ 5 k $, where $ k $ is a positive integer.
Applying Pythagoras theorem in $ \triangle \mathrm{ABC} $, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$(12 k)^{2}=(5 k)^{2}+B C^{2}$
$144 k^{2}=25 k^{2}+B C^{2}$
$B C^{2}=119 k^{2}$
$B C=10.9 k$
It can be observed that for given two sides $ A C=12 k $ and $ A B=5 k $, BC should be such that,
$\mathrm{AC}-\mathrm{AB} < \mathrm{BC} < \mathrm{AC}+\mathrm{AB}$
$12 \mathrm{k}-5 \mathrm{k} < \mathrm{BC} < 12 \mathrm{k}+5 \mathrm{k}$
$7 \mathrm{k} < \mathrm{BC} < 17 \mathrm{k}$
However, $ B C=10.9 \mathrm{k} $. Clearly, such a triangle is possible and hence, such value of $ \sec A $ is possible.
Hence, the given statement is true.

(iii) State whether the following are true or false. Justify your answer.
$ \cos A $ is the abbreviation used for the cosecant of angle A .

Answer

Abbreviation used for cosecant of angle A is $ \operatorname{cosec} \mathrm{A} $. And $ \cos \mathrm{A} $ is the abbreviation used for cosine of angle A.
Hence, the given statement is false.

(iv) State whether the following are true or false. Justify your answer.
$ \cot \mathrm{A} $ is the product of $ \cot $ and A

Answer

$ \cot A $ is not the product of $ \cot $ not $ A $. It is the cotangent of $ \angle A $.
Hence, the given statement is false.

(v) State whether the following are true or false. Justify your answer.
$ \sin \theta=\frac{4}{3} $, for some angle $ \theta $

Answer

$ \sin \theta=\frac{4}{3} $
We know that in a right-angled triangle,
$\sin \theta=\frac{\text { Side opposite to } \angle \theta}{\text { Hypotenuse }}$
In a right-angled triangle, hypotenuse is always greater than the remaining two sides.
Therefore, such value of $ \sin \theta $ is not possible.
Hence, the given statement is false.

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now

CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1 || NCERT Solutions for Class 10 Maths Chapter 8: Introduction to Trigonometry(English Medium)

Download the Math Ninja App Now