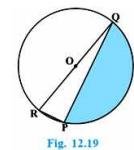
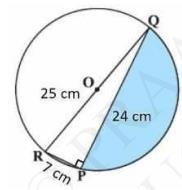
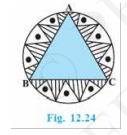
6. In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).

Answer
Radius of the circle "R" \( =32 \mathrm{~cm} \)Draw a median AD of the triangle passing through the centre of the circle.
\(\Rightarrow \mathrm{BD}=\frac{ \mathrm{AB} }{ 2 }\)
Since, AD is the median of the triangle
\( \therefore \mathrm{AO}= \) Radius of the circle \( =\frac{ 2 }{ 3 } \mathrm{AD} \) [By the property of equilateral triangle inscribed in a circle]
\(\Rightarrow \frac{ 2 }{ 3 } \mathrm{AD}=32 \mathrm{~cm}\)
\( \Rightarrow \mathrm{AD}=48 \mathrm{~cm} \)
In \( \triangle \mathrm{ADB} \)
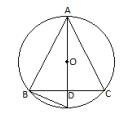
By Pythagoras theorem,
\(\mathrm{AB}^{2}=\mathrm{AD}^{2}+\mathrm{BD}^{2}\)
\(\Rightarrow \mathrm{AB}^{2}=48^{2}+(\frac{ \mathrm{AB} }{ 2 })^{2}\)
\(\Rightarrow \mathrm{AB}^{2}=2304+\frac{ \mathrm{AB}^{2} }{ 4 }\)
\(\Rightarrow \frac{ 3 }{ 4 }\left(\mathrm{AB}^{2}\right)=2304\)
\(\Rightarrow \mathrm{AB}^{2}=3072\)
\(\Rightarrow \mathrm{AB}=32
{\sqrt{3}} \mathrm{~cm}\)
Area of \( \triangle \mathrm{ABC}=
\frac{ {\sqrt{3}} }{ 4 } \times(32 \sqrt{3})^{2} \mathrm{~cm}^{2} \)
\(=768
{\sqrt{3}} \mathrm{~cm}^{2}\)
Area of circle \( =\pi \mathrm{R}^{2} \)
\(=\frac{ 22 }{ 7 } \times 32 \times 32=\frac{ 22528 }{ 7 } \mathrm{~cm}^{2}\)
Area of the design \( = \) Area of circle - Area of \( \triangle \mathrm{ABC} \)
\( =(\frac{ 22528 }{ 7 }-768 {\sqrt{3}}) \mathrm{cm}^{2} \)
CBSE Solutions for Class 10 Maths Chapter 12: Areas Related to Circles || CBSE Class 10 Maths Chapter 12 Areas Related to Circles solutions Ex 12.3
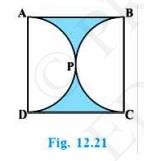
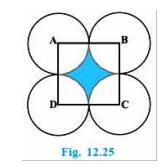
Download the Math Ninja App Now7. In Fig. 12.25, ABCD is a square of side 14 cm. With centers \(A , B, C \) and \( D \), four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.

Answer
To Find: Area of shaded regionGiven: Side of square \( \mathrm{ABCD}=14 \mathrm{~cm} \)
Radius of circles with centers \( A, B, C \) and \( D=\frac{14}{ 2}=7 \mathrm{~cm} \)
Area of shaded region \( = \) Area of square - Area of four sectors subtending right angle
Area of each of the 4 sectors is equal to each other and is a sector of \( 90^{\circ} \) in a circle of 7 cm radius. So, Area of four sectors will be equal to Area of one complete circle
Area of 4 sectors \( =\pi \mathrm{r}^{2} \)
Area of 4 sectors \( =\frac{22}{7} \times 7 \times 7 \)
Area of 4 sectors \( =154 \mathrm{~cm}^{2} \)
Area of square \( \mathrm{ABCD}\)=(Side)\(^{2} \)
Area of square \( \mathrm{ABCD}=(14)^{2} \)
Area of square \( \mathrm{ABCD}=196 \mathrm{~cm}^{2} \)
Area of shaded portion \( = \) Area of square \( \mathrm{ABCD} - 4 \times \) Area of each sector
\(=196-154\)
\(=42 \mathrm{~cm}^{2}\)
Therefore, the area of shaded portion is \( \mathbf{4 2} \mathbf{~ c m}^{2} \)
CBSE Solutions for Class 10 Maths Chapter 12: Areas Related to Circles || CBSE Class 10 Maths Chapter 12 Areas Related to Circles solutions Ex 12.3
Download the Math Ninja App Now8. Fig. 12.26 depicts a racing track whose left and right ends are semicircular.
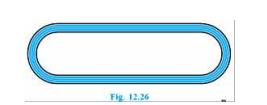
The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track.

The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) The distance around the track along its inner edge
(ii) The area of the track.
Answer
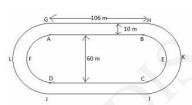
(i) Distance around the track along its inner edge \( =\mathrm{AB}+ \) semicircle \( \mathrm{BEC}+\mathrm{CD}+ \) semicircle \( \mathrm{DFA}\)
\( =106+\left(\frac{1}{2} \times 2 \pi r\right) \)
CBSE Solutions for Class 10 Maths Chapter 12: Areas Related to Circles || CBSE Class 10 Maths Chapter 12 Areas Related to Circles solutions Ex 12.3
Download the Math Ninja App NowCentral Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.3
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.5
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.6
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.1
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.2
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.4
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4
Class 10 : NCERT Solutions for Class 10 Maths Chapter 9
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2