8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is \( 60^{\circ} \) and from the same point the angle of elevation of the top of the pedestal is \( 45^{\circ} \). Find the height of the pedestal.
Answer
Let AD be the height of the statue which is 1.6 m , And DB be the height of the pedestal.And C be the point where the observer is present.
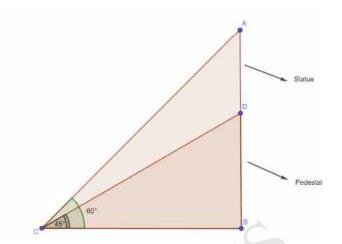
To find: height of pedestal, BD
Now,
In \( \Delta \mathrm{ABC} \),
\( \tan \theta=\frac{p}{b} \)
where \( \mathrm{p}= \) perpendicular and \( \mathrm{b}= \) base
\( \tan 60^{\circ}=\frac{p}{b} \)
\( \sqrt{3}=\frac{D B+1.6}{b} \)
\( b=\frac{D B+1.6}{\sqrt{3}} \ldots\) (i)
In \( \triangle D B C \),
\( \tan \theta=\frac{p}{b} \)
\( \tan 45^{\circ}=\frac{p}{b} \)
\( 1=\frac{D B}{b} \)
\( b=\mathrm{DB} \ldots\) (ii)
On comparing (i) and (ii),
\(D B=\frac{D B+1.6}{\sqrt{3}}\)
\(
D B \sqrt{3}=D B+1.6\)
\(D B(\sqrt{3}-1)=1.6\)
\(D B=\frac{1.6}{\sqrt{3}-1}\)
\(D B=\frac{1.6}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\)
\(D B=\frac{1.6 \times(\sqrt{3}+1)}{3-1}\)
\(D B=0.8(\sqrt{3}+1)
\)
Hence, height of pedestal is \( 0.8(\sqrt{3}+1) \mathrm{m} \).
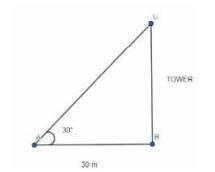
9. The angle of elevation of the top of a building from the foot of the tower is \( 30^{\circ} \) and the angle of elevation of the top of the tower from the foot of the building is \( 60^{\circ} \). If the tower is 50 m high, find the height of the building.


Answer
Let us take AB as building and Let us take DC as tower \( =50 \mathrm{~m} \), \( \angle \mathrm{ACB}=30^{\circ} \)And,
\(
\angle \mathrm{DBC}=60^{\circ},
\)
\( \mathrm{AB}= \) ?
In \( \Delta \) DCB;
\( \tan \theta=\frac{p}{b} \)
where, \( \mathrm{p}= \) perpendicular and \( \mathrm{b}= \) base
\( \tan 60^{\circ}=\frac{50}{b} \)
\( \sqrt{3}=\frac{50}{b} \)
\( b=\frac{50}{\sqrt{3}} \)
In \( \Delta \mathrm{ACB} \)
\( \tan \theta=\frac{p}{b} \)
where \( \mathrm{p}= \) perpendicular and \( \mathrm{b}= \) base
\( \tan 30^{\circ}=\frac{A B}{b} \)
\(
\frac{1}{\sqrt{3}}=\frac{A B}{\frac{50}{\sqrt{3}}}\)
\(A B=\frac{50}{\sqrt{3} \times \sqrt{3}}\)
\(\mathrm{AB}=16.67 \mathrm{~m}
\)
10. Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are \( 60^{\circ} \) and \( 30^{\circ} \), respectively. Find the height of the poles and the distances of the point from the poles.


Answer
Let AB and DE be the two poles, and C be the point of observation. Given, width of road, \( \mathrm{BD}=80 \mathrm{~m} \) Angle of elevation to \( \mathrm{AB}, \angle \mathrm{ACB}= \) \( 30^{\circ} \) Angle of elevation to \( \mathrm{DE}, \angle \mathrm{ECD}=60^{\circ} \) To find: Height of buildings AB and DE .In \( \Delta \mathrm{ACB} \)
\( \tan \theta=\frac{p}{b} \)
\( \tan 30^{\circ}=\frac{A B}{B C} \)
\( \frac{1}{\sqrt{3}}=\frac{A B}{B C} \)
\( A B=\frac{B C}{\sqrt{3}} \ldots \) (i)
In \( \triangle E D C \)
\( \tan \theta=\frac{p}{b} \)
\( \tan 60^{\circ}=\frac{E D}{C D} \)
\( \sqrt{3}=\frac{E D}{80-B C} \)
\( E D=\sqrt{3}(80-B C) \ldots\) (ii)
We know that \( \mathrm{AB}=\mathrm{ED} \) as the poles are of same height.
Hence, from (i) and (ii),
\(
\frac{B C}{\sqrt{3}}=\sqrt{3}(80-B C)
\)
cross multiplying, we get
\(
\mathrm{BC}=3(80-\mathrm{BC})\)
\(\mathrm{BC}=240-3 \mathrm{BC}\)
\(4 \mathrm{BC}=240\)
\(\mathrm{BC}=60 \mathrm{~m}
\)
Now using the value of BC in (i),
\(
\mathrm{AB}=20 \sqrt{3} \mathrm{~m}\)
\(\tan 60^{\circ}=\frac{E D}{C D}
\)
Now from triangle EDC, \( \sqrt{3}=\frac{20 \sqrt{3}}{C D} \)
\(
\mathrm{CD}=20 \mathrm{~m}
\)
Therefore, Height of Pole \( =20 {\sqrt{3}} \mathrm{~m} \). Distances of poles from observing point \( =60 \mathrm{~m} \) and \( 20\) m
CBSE Solutions for Class 10 Maths Chapter 9: Some Applications of Trigonometry || CBSE Class 10 Maths Chapter 9 Some Applications of Trigonometry solutions
Download the Math Ninja App Now
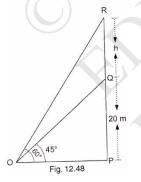
11. A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is \( 60^{\circ} \). From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is \( 30^{\circ} \) (see Fig. 9.12). Find the height of the tower and the width of the canal.


Answer
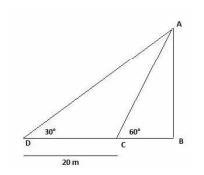
According to this figure:
\( \mathrm{CD}=20 \mathrm{~m}, \)
\( \angle \mathrm{ACB}=60^{\circ} \),
\( \angle \mathrm{ADB}=30^{\circ} \),
\( \mathrm{AB}= \) ? and \( \mathrm{BD}= \) ?
In \( \Delta \mathrm{ABC} \),
\( \tan \theta=\frac{p}{b} \)
where \( \mathrm{p}= \) perpendicular and \( \mathrm{b}= \) base of triangle
\( \tan 60^{\circ}=\frac{A B}{B C} \)
\( \sqrt{3}=\frac{A B}{B C} \)
\( A B=\sqrt{3} B C \ldots\) (i)
In \( \Delta \mathrm{ABD} \),
\( \tan \theta=\frac{p}{b} \)
\( \tan 30^{\circ}=\frac{A B}{B C+20} \)
\( \frac{B C+20}{\sqrt{3}}=A B \ldots\) (ii)
From (i) and (ii),
\( \sqrt{3}(B C)=\frac{B C+20}{\sqrt{3}} \)
\(
3 \mathrm{BC}=\mathrm{BC}+20\)
\(\mathrm{BC}=10 \mathrm{~m}
\)
Using the value of BC in (i) we get;
\( \mathrm{AB}=10 {\sqrt{3}} \mathrm{~m} \) which is the height of the tower
Width of canal \( =10 \mathrm{~m} \)
12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is \( 60^{\circ} \) and the angle of depression of its foot is \( 45^{\circ} \). Determine the height of the tower.


Answer
Let us take AB as a building, with \( \mathrm{AB}=7 \) mand CE as a cable tower. Angle of elevation from top of tree to top of cable tower \( \angle E A D= \) \( 60^{\circ} \), and angle of depression from the top of the building to the bottom of the tower is, \( \angle \mathrm{CAD}=45^{\circ} \) Also, \( \angle \mathrm{CAD}=\angle \mathrm{ACB} \) [Alternate angles]Clearly,
\( \mathrm{AB}=\mathrm{DC} \) and \( \mathrm{EC}=\mathrm{ED}+\mathrm{DC} \) ?
In \( \triangle \mathrm{ABC} \) :
\(
\tan \theta=\frac{p}{b}
\)
where \( \mathrm{p}= \) perpendicular and \( \mathrm{b}= \) base, therefore \( \tan 45^{\circ}=\frac{A B}{B C} \)
\( \mathrm{AB}=\mathrm{BC}=7 \mathrm{~m} \)
In \( \Delta \mathrm{EDA} \),
\(
\tan \theta=\frac{p}{q}\)
\(\tan 60^{\circ}=\frac{E D}{7}\)
\(\sqrt{3}=\frac{E D}{7}\)
\(E D=7 {\sqrt{3}} m
\)
However,
The height of tower can be calculated as:
\(
\mathrm{EC}=\mathrm{ED}+\mathrm{DC}\)
\(=7 {\sqrt{3}}+7\)
\(=7({\sqrt{3}}+1) \mathrm{m}
\)
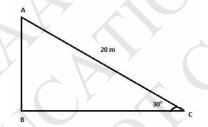
13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are \( 30^{\circ} \) and \( 45^{\circ} \). If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Answer

A and D are the two ships and the distance between the ships is AD . BC is the lighthouse and is the height of the lighthouse. Observer is at point C
Give: \( \mathrm{BC}= \) height of lighthouse \( =75 \mathrm{~m} \)
\( \angle \mathrm{CAB}=45^{\circ} \),
\( \angle \mathrm{CDB}=30^{\circ} \)
To Find: DA
In \( \Delta \mathrm{ABC} \),
\( \tan \theta=\frac{p}{b} \)
[ \( p= \) perpendicular and \( b= \) base of the right angled triangle]
\(
\tan \left(45^{\circ}\right)=\frac{75}{A B}\)
\(\mathrm{AB}=75 \mathrm{~m} \quad\left[\tan 45^{\circ}=1\right]\)
In \( \Delta \mathrm{CDB} \),
\(
\tan \theta=\frac{p}{b}\)
\(\tan 30^{\circ}=\frac{75}{B D}\)
\(\frac{1}{\sqrt{3}}=\frac{75}{B D}\)
\(B D=75 \sqrt{3} m\)
\(A D+A B=75 \sqrt{3} \mathrm{~m}\)
\(D A=75 \sqrt{3}-75\)
\(D A=75(\sqrt{3}-1) m
\)
Hence the distance between the ships is \( 75(\sqrt{3}-1) \mathrm{m} \mathrm{m} \)
CBSE Solutions for Class 10 Maths Chapter 9: Some Applications of Trigonometry || CBSE Class 10 Maths Chapter 9 Some Applications of Trigonometry solutions
Download the Math Ninja App Now14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is \( 60^{\circ} \).
After some time, the angle of elevation reduces to \( 30^{\circ} \) (see Fig. 9.13). Find the distance travelled by the balloon during the interval.

After some time, the angle of elevation reduces to \( 30^{\circ} \) (see Fig. 9.13). Find the distance travelled by the balloon during the interval.

Answer

From this figure:
\( \mathrm{BF}= \) height of girl \( =1.2 \mathrm{~m} \),
\( A G= \) height of balloon from ground initially \( =88.2 \mathrm{~m} \),
\( \mathrm{AC}=\mathrm{AG}-\mathrm{GC} \)
\( =88.2-1.2 \)
\( =87 \mathrm{~m} \)
\( \angle \mathrm{EBD}=30^{\circ} \) and \( \angle \mathrm{ABC}=60^{\circ} \),
\( \mathrm{CD}= \) ?
In \( \triangle \mathrm{ABC} \);
\( \tan \theta=\frac{p}{b} \)
where \( \mathrm{p}= \) perpendicular and b is base
\(
\tan 60^{\circ}=\frac{87}{B C}\)
\(\sqrt{3}=\frac{87}{B C}\)
\(B C=\frac{87}{\sqrt{3}}
\)
In \( \triangle A B C \)
\(
\tan \theta=\frac{p}{b}\)
\(\tan 30^{\circ}=\frac{87}{B D}\)
\(\frac{1}{\sqrt{3}}=\frac{87}{B D}\)
\(B D=87 \sqrt{3}
\)
Now, the distance covered by the balloon will be:
\(
\mathrm{CD}=\mathrm{BD}-\mathrm{BC}\)
\(C D=87 \sqrt{3}-\frac{87}{\sqrt{3}}\)
\(C D=\frac{87 \times 3-87}{\sqrt{3}}\)
\(C D=\frac{174}{\sqrt{3}}
\)
Now for rationalizing, multiply and divide by \( \sqrt{3} \)
\(
C D=\frac{174}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
\(C D=\frac{174}{3} \times \sqrt{3}\)
\(C D=58 \sqrt{3}\)
\(C D=58 \sqrt{3} \mathrm{~m}
\)
15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of \( 30^{\circ} \), which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be \( 60^{\circ} \). Find the time taken by the car to reach the foot of the tower from this point.
Answer
The diagram is: 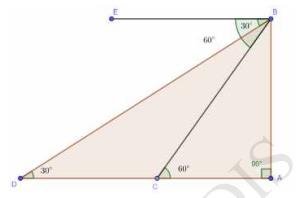
Let \( A B \) is the tower and \( A D \) is the highway.
Now from triangle ADB ,
\(
\tan 30^{\circ}=\frac{ A B }{ A D }\)
\(\Rightarrow \frac{ 1 }{ {\sqrt{3}} }=\frac{ \mathrm{AB} }{ \mathrm{AD }}\)
\(\Rightarrow \mathrm{AB}=\frac{ \mathrm{AD} }{ {\sqrt{3}} }
\) \(\dots\dots\dots\)(1)
Again from triangle ACB
\( \tan 60^{\circ}=\frac{ \mathrm{AB} }{ \mathrm{AC}}\)
\(\Rightarrow {\sqrt{3}}=\frac{ \mathrm{AB} }{ \mathrm{AC} }\)
\(\Rightarrow \mathrm{AB}=\mathrm{AC} {\sqrt{3}}
\) \(\dots\dots..\)(2)
from equation 1 and 2
\( \frac{ \mathrm{AD} }{ {\sqrt{3}} } = \mathrm{AC} {\sqrt{3}}\)
\(\Rightarrow \frac{ (\mathrm{DC}+\mathrm{CA}) }{ {\sqrt{3}} }=\mathrm{AC} {\sqrt{3}}\)
\(\Rightarrow \mathrm{DC}+\mathrm{CA}=\mathrm{AC} {\sqrt{3}} \times {\sqrt{3}}\)
\(\Rightarrow \mathrm{DC}+\mathrm{CA}=3 \mathrm{AC}\)
\(\Rightarrow 3 \mathrm{AC}-\mathrm{AC}=\mathrm{CD}
\)
\(
\Rightarrow 2 \mathrm{AC}=\mathrm{CD}\)
\(\Rightarrow \mathrm{AC}=\frac{ \mathrm{CD} }{ 2 }
\)
Since time taken by car to cover \( \mathrm{CD}=6 \) Second
So time taken by car to cover \( \mathrm{AC}=\frac{ 6 }{ 2 }=3 \) seconds.
16. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Answer

Let \( \angle \mathrm{ADB}=\theta \) and \( \angle \mathrm{ACB}=90^{\circ}-\theta \)
[ As angles are complementary, their sum will be equal to \( 90^{\circ} \), and if one is \( \theta \) other will be \( \left.90^{\circ}-\theta\right] \) In \( \Delta \mathrm{ABD} \);
\( \tan \theta=\frac{A B}{D B} \)
\( \tan \theta=\frac{A B}{9} \)
In \( \triangle A B C \)
\( \tan (90-\theta)=\frac{A B}{B C} \)
\( \cot \theta=\frac{A B}{4} \)
But we know that,
\( \cot \theta=\frac{1}{\tan \theta} \)
And also by complementary angle formula that \( \tan \left(90^{\circ}-\theta\right)=\cot \theta \) \( \tan (\theta) \tan \left(90^{\circ}-\theta\right)=1 \)
\( \tan \left(90^{\circ}-\theta\right)=\frac{1}{\tan \theta} \)
Therefore,
\(
\frac{A B}{4}=\frac{9}{A B}
\)
\( \mathrm{AB}^{2}=36 \)
\( \mathrm{AB}=6 \mathrm{~m} \)
Hence proved.
CBSE Solutions for Class 10 Maths Chapter 9: Some Applications of Trigonometry || CBSE Class 10 Maths Chapter 9 Some Applications of Trigonometry solutions
Download the Math Ninja App NowCentral Board of Secondary Education Official Site
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 1 Exercise 1.3
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.1
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.2
Class 10 : CBSE Class 10 Maths Chapter 2 Polynomials Ex 2.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.2
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.3
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.4
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.5
Class 10 : CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables solutions Ex 3.6
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.2
Class 10 : CBSE Class 10 Maths Chapter 4 Quadratic Equations Ex 4.3
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2
Class 10 : CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.3
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.1
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.2
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.3
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.4
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.5
Class 10 : CBSE Class 10 Maths Chapter 6 Triangle Ex 6.6
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.1
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.2
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.3
Class 10 : CBSE Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.1
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.2
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.3
Class 10 : NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4
Class 10 : CBSE Class 10 Maths Chapter 10 Circles solutions Ex 10.2
Class 10 : CBSE Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.2