CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Get the complete NCERT Solutions for Class 10 Maths Chapter 11 : Constructions, covering Exercise 11.1. This free resource helps you understand key concepts and solve problems with ease, perfect for CBSE Class 10 students preparing for exams using NCERT Maths materials. We hope the NCERT Solutions for Class 10 Maths Chapter 11 Constructions Exercise 11.1 help you. If you have any queries regarding NCERT Maths Solutions Chapter 11 Constructions Exercise 11.1, drop a comment below, and we will get back to you at the earliest.

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1
Exercise 11.1

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

1. Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.

Answer

Steps of construction:
i. At first, we will draw a line segment $ \mathrm{AB}=7.6 \mathrm{~cm} $.

ii. Draw a ray AX such that it makes an acute angle with AB .

iii. Now, locate 13 points $ (5+8) \mathrm{A}_{1}, \mathrm{~A}_{2},
\mathrm{~A}_{3}, \ldots \ldots . \mathrm{A}_{13} $ on AX so that;
$\mathrm{AA}_{1}=\mathrm{A}_{1}\mathrm{~A}_{2}=\mathrm{A}_{2} \mathrm{~A}_{3}=\mathrm{A}_{3} \mathrm{~A}_{4}=\mathrm{A}_{4} \mathrm{~A}_{5}=\mathrm{A}_{5} \mathrm{~A}_{6}=\mathrm{A}_{6} \mathrm{~A}_{7}=\mathrm{A}_{7} \mathrm{~A}_{8}=\mathrm{A}_{8} \mathrm{~A}_{9}=$
$\mathrm{A}_{9} \mathrm{~A}_{10}=\mathrm{A}_{10} \mathrm{~A}_{11}=\mathrm{A}_{11} \mathrm{~A}_{12}=\mathrm{A}_{12} \mathrm{~A}_{13}$

iv. Join $ \mathrm{A}_{13} $ to B
v. Draw a line $ A_{5} C \| A_{13} B $; which intersects $ A B $ at point $ C $ and passes Through the point $ A_{5} $.
Now we have, $\mathrm{AC} : \mathrm{CB}=5: 8 $
On measuring with the scale.
$\mathrm{AC}=2.92 \mathrm{~cm}$
And
$\mathrm{CB}=4.68 \mathrm{~cm}$
Justification:
Since $ \angle \mathrm{AA}_{13} \mathrm{~B}=\angle \mathrm{AA}_{5} \mathrm{C} $
With $ A X $ is a transversal, corresponding angles are equal, Hence $ \mathrm{A}_{13} \mathrm{~B} $ and $ \mathrm{A}_{5} \mathrm{C} $ are parallel.
So by basic proportionality theorem, $ \frac{A A_{5}}{A_{5} A_{13}}=\frac{A C}{C B} $
By construction $ \frac{A A_{5}}{A_{5} A_{13}}=\frac{5}{8} $
So, $ \frac{A C}{C B}=\frac{5}{8} $
Hence C divides AB in the ratio 5:8.

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

2. Construct a triangle of sides $ 4 \mathrm{~cm}, 5 \mathrm{~cm} $ and $6\mathrm{~cm}$ and then a triangle similar to it whose sides are $ \frac{2}{3} $ of the corresponding sides of the first triangle.

Answer

Steps of construction:
i. Now in order to make a triangle, draw a line segment $ \mathrm{AB}=4 \mathrm{~cm} $.

ii. Then, draw an arc at $5$ cm from point A. From point B, draw an arc at $6$ cm in such a way that it intersects the previous arc. Join the point of intersection from points A and B. This gives the required triangle ABC.

iii. Now, divide the base in the ratio $ 2: 3 $. Draw a ray $ A X $ which is at an acute angle from $ A B $. Then, plot three points on $ A X $ such that; $ \mathrm{AA}_{1}=\mathrm{A}_{1} \mathrm{~A}_{2}=\mathrm{A}_{2} \mathrm{~A}_{3} $. Join $ \mathrm{A}_{3} $ to B .
iv. Draw a line from point $ A_{2} $ parallel to $ A_{3} B $ and intersects $ A B $ at point $ B^{\prime} $.
v. Draw a line from point $ B^{\prime} $ that is parallel to $BC$ intersecting $AC$ at point $ C^{\prime} $.

Hence, triangle $ \mathrm{AB}^{\prime} \mathrm{C}^{\prime} $ is the required triangle.
justification:

Since the scalar factor is $ \frac{ 2 }{ 3 } $
We need to prove:
$ \frac{A B^{\prime}}{A B}=\frac{A C^{\prime}}{A C}=\frac{B^\prime C^{\prime}}{B C}=\frac{2}{3} $
By construction,
$\frac{A B^{\prime}}{A B}=\frac{A A_{2}}{A A_{3}}=\frac{2}{3} \ldots(1)$
Also, $ B^{\prime} C^{\prime} $ is parallel to $BC$.
So, both will make same angle with $AB$.
$ \therefore \angle \mathrm{AB}^{\prime} \mathrm{C}^{\prime}=\angle \mathrm{ABC} $ (corresponding angles)
In $ \Delta \mathrm{AB}^{\prime} \mathrm{C}^{\prime} $ and $ \Delta \mathrm{ABC} $
$\angle \mathrm{A}=\angle \mathrm{A}(\text { common })$$\angle \mathrm{AB}^{\prime} \mathrm{C}^{\prime}=\angle \mathrm{ABC}$
So, by $AA$ similarity
$\Delta \mathrm{AB}^{\prime} \mathrm{C}^{\prime} \sim \Delta \mathrm{ABC}$
As we know if two triangles are similar the ratio of their corresponding sides are also equal.
So,
$\frac{A B^{\prime}}{A B}=\frac{A C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}$
From (1),
$\frac{A B^{\prime}}{A B}=\frac{A C^{\prime}}{A C}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{2}{3}$
Hence proved.

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

3. Construct a triangle with sides $ 5 \mathrm{~cm}, 6 \mathrm{~cm} $ and 7 cm and then another triangle whose sides are $ \frac{7}{5} $ of the corresponding sides of the first triangle.

Answer

1. Now in order to make a triangle, draw a line segment $ A B $ $ =5 \mathrm{~cm} $. From point A, draw an arc at 6 cm. Draw an arc at 7 cm from point $ B $ intersecting the previous arc.

2. Join the point of intersection from A and B .

Hence, this gives the required triangle ABC
3. Dividing the base, draw a ray $AX$ which is at an acute angle from AB

4. Plot seven points on $ A X $ such that:
$\mathrm{AA}_{1}=\mathrm{A}_{1} \mathrm{~A}_{2}=\mathrm{A}_{2} \mathrm{~A}_{3}=\mathrm{A}_{3} \mathrm{~A}_{4}=\mathrm{A}_{4} \mathrm{~A}_{5}=\mathrm{A}_{5} \mathrm{~A}_{6}=\mathrm{A}_{6} \mathrm{~A}_{7}$

5. Join $ \mathrm{A}_{5} $ to B .
6. Draw a line from point $ \mathrm{A}_{7} $ that is parallel to $ \mathrm{A}_{5} \mathrm{B} $ and joins $ \mathrm{AB}^{\prime}(\mathrm{AB} $ extended to $ \left.\mathrm{AB}^{\prime}\right) $.
7. Draw a line $ \mathrm{B}^{\prime} \mathrm{C}^{\prime} \| \mathrm{BC} $.

Hence, triangle $ \mathrm{AB}^{\prime} \mathrm{C}^{\prime} $ is the required triangle.

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

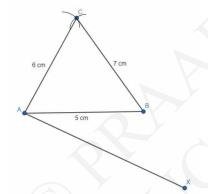
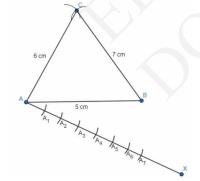
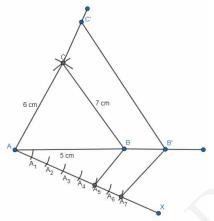
4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are $ 1 \frac{1}{2} $ times the corresponding sides of the isosceles triangle.

Answer

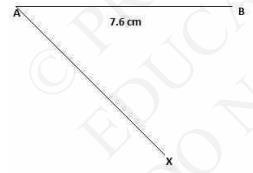
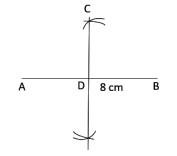
Steps of construction:
i. Now in order to make a triangle, draw a line segment $ \mathrm{AB}=8 \mathrm{~cm} $.

ii. Draw two arcs intersecting at 4 cm distance from points A and B; on either side of AB.
Join these arcs to get perpendicular bisector CD of AB. (Since, altitude is the perpendicular bisector of base of isosceles triangle).

iii. Join points $ A $ and $ B $ to $ C $ in order to get the triangle $ A B C $.

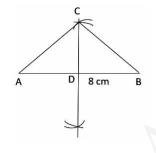
iv. Now, draw a ray AX which is at an acute angle from point A .
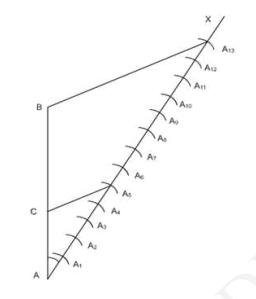
As $ 1 \frac{1}{2}=\frac{3}{2} $
And 3 is greater between 3 and 2, So Plot 3 points on $AX$ such that: $ \mathrm{AA}_{1}=\mathrm{A}_{1} \mathrm{~A}_{2}=\mathrm{A}_{2} \mathrm{~A}_{3} $.

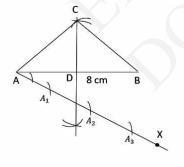
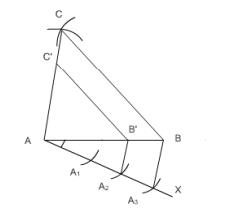
v. As 2 is smaller between 2 and 3 . Join $ \mathrm{A}_{2} $ to point B . Draw a line from $ \mathrm{A}_{3} $ which is parallel to $ \mathrm{A}_{2} \mathrm{~B} $ meeting the extension of $ A B $ at $ B^{\prime} $.

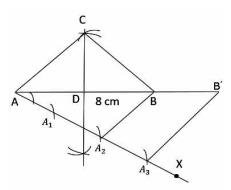
vi. Draw $ \mathrm{B}^{\prime} \mathrm{C}^{\prime} \| \mathrm{BC} $. Then, draw $ \mathrm{A}^{\prime} \mathrm{C}^{\prime} \| \mathrm{AC} $.

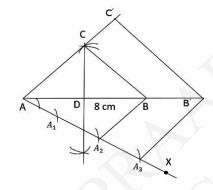
Triangle $ \mathrm{AB}^{\prime} \mathrm{C}^{\prime} $ is the required triangle.
Justification:
We need to prove,
$ \frac{A C \prime}{A C}=\frac{A B \prime}{A B}=\frac{C \prime B \prime}{C B}=\frac{3}{2} $
By construction $ \frac{A B^{\prime}}{A B}=\frac{A A_{3}}{A A_{2}}=\frac{3}{2} $ $\quad\dots.$(1)
$s C'B'\| CB$
They will maker equal angles with line $ \mathrm{AB} \angle \mathrm{ACB}=\angle \mathrm{AC}^{\prime} \mathrm{B}^{\prime} $$\quad \dots.$ (corresponding angles)
In $ \triangle \mathrm{ACB} $ and $ \triangle \mathrm{AC}^{\prime} \mathrm{B}^{\prime} $
$ \angle \mathrm{A}=\angle \mathrm{A} $ (common) $ \angle \mathrm{ACB}=\angle \mathrm{AC} \mathrm{B}^{\prime} $ (corresponding angles)
So $ \triangle \mathrm{ACB} \sim \triangle \mathrm{AC}^{\prime} \mathrm{B}^{\prime} $
As corresponding sides of similar triangles are in ratio, Hence, $ \frac{A C \prime}{A C}= $ $ \frac{A C^{\prime}}{A C}=\frac{A B \prime}{A B}=\frac{C \prime B \prime}{C B}=\frac{3}{2} $

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

$Mathninja.in$

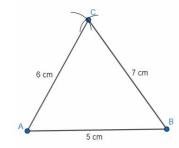
5. Draw a triangle $ A B C $ with side $ B C=6 \mathrm{~cm}, A B=5 \mathrm{~cm} $ and $ \angle A B C=60^{\circ} $. Then construct a triangle whose sides are $ \frac{3}{4} $ of the corresponding sides of the triangle ABC .

Answer

Given in $ \Delta \mathrm{ABC} $,
Length of side $ \mathrm{BC}=6 \mathrm{~cm} $.
Length of side $ \mathrm{AB}=5 \mathrm{~cm} $.
$ \angle \mathrm{ABC}=60^{\circ} $.
Steps of Construction:
1. Draw a line segment BC of length 6 cm .

2. With B as center, draw a line which makes an angle of $ 60^{\circ} $ with BC.
Construction of $ 60^{\circ} $ angle at B:
a. With B as centre and with some convenient radius draw an arc which cuts the line BC at
D.

b. With D as radius and with same radius (in step a), draw another arc which cuts the previous arc at E.

c. Join BE. The line BE makes an angle $ 60^{\circ} $ with BC.

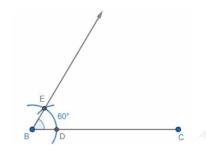
3. Again with $ B $ as centre and with radius of 5 cm , draw an arc which intersects the line BE at point A .

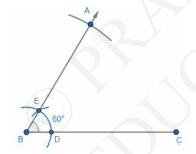
4. Join AC. This is the required triangle.

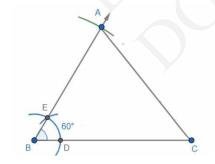
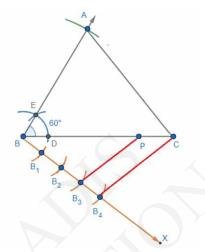
5. Now, from B , draw a ray BX which makes an acute angle on the opposite side of the vertex $ A $.

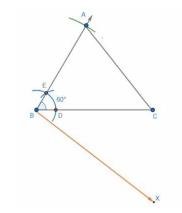
6. With $ B $ as center, mark four points $ B_{1}, B_{2}, B_{3} $ and $ B_{4} $ on $ B X $ such that they are equidistant. i.e. $ \mathrm{BB}_{1}=\mathrm{B}_{1} \mathrm{~B}_{2}=\mathrm{B}_{2} \mathrm{~B}_{3}=\mathrm{B}_{3} \mathrm{~B}_{4} $.

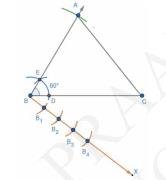
7. Join $ B_{4} C $ and then draw a line from $ B_{3} $ parallel to $ B_{4} C $ which meets the line BC at P .

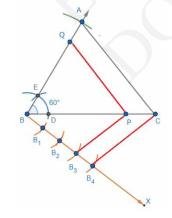
8. From $ P $, draw a line parallel to $ A C $ and meets the line $ A B $ at $ Q $. Thus $ \triangle \mathrm{BPQ} $ is the required triangle.

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

6. Draw a triangle $ABC$ with side $ \mathrm{BC}=7 \mathrm{~cm}, \angle \mathrm{B}=45^{\circ}, \angle \mathrm{A}= $ $ 105^{\circ} $. Then, construct a triangle whose sides are $ \frac{4}{3} $ times the corresponding sides of $ \triangle \mathrm{ABC} $.

Answer

Steps of construction:
1. Draw a line segment $ \mathrm{BC}=7 \mathrm{~cm} $.

2. Draw $ \angle \mathrm{ABC}=45^{\circ} $ and $ \angle \mathrm{ACB}=30^{\circ} $ i.e. $ \angle \mathrm{BAC}=105^{\circ} $.

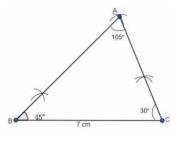
We obtain $ \triangle \mathrm{ABC} $.
3. Draw a ray $BX$ making an acute angle with BC. Mark four points $ \mathrm{B}_{1}, \mathrm{~B}_{2}, \mathrm{~B}_{3}, \mathrm{~B}_{4} $ at equal distances.

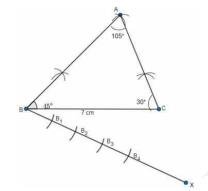
4. Through $ \mathrm{B}_{3} $ draw $ \mathrm{B}_{3} \mathrm{C} $ and through $ \mathrm{B}_{4} $ draw $ \mathrm{B}_{4} \mathrm{C}_{1} $ parallel to $ \mathrm{B}_{3} \mathrm{C} $. Then draw $ \mathrm{A}_{1} \mathrm{C}_{1} $ parallel to AC.

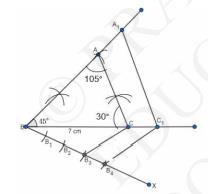
$ \therefore \mathrm{A}_{1} \mathrm{BC}_{1} $ is the required triangle.

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm . Then construct another triangle whose sides are $ \frac{5}{3} $ times the corresponding sides of the given triangle.

Answer

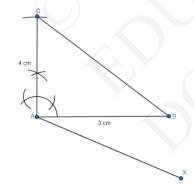
Steps of construction:
1. Now in order to make a triangle, draw a line segment $ \mathrm{AB}=3 $ cm .

2. Make a right angle at point A and draw $ \mathrm{AC}=4 \mathrm{~cm} $ from this point.

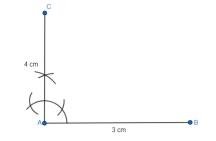
3. Join points $ A $ and $ B $ to get the right triangle $ A B C $.

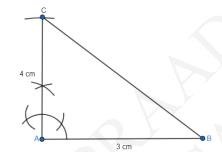
4. Now, Dividing the base, draw a ray $AX$ such at it forms an acute angle from $ A B $.

5. Then, plot 5 points on $ A X $ such that: $\mathrm{AG}=\mathrm{GH}=\mathrm{HI}=\mathrm{IJ}=\mathrm{JK} .$

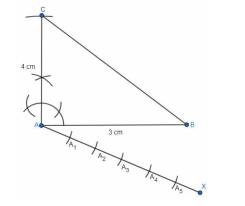
6. Join I to point line $ A B $ and Draw a line from $K$ which is parallel to $IB$ such that it meets $AB$ at point $M$ .
7. Draw $ \mathrm{MN} \| \mathrm{CB} $.

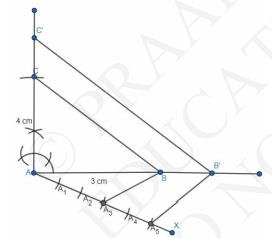
This is the required construction, thus forming $AMN$ which have all the sides $ \frac{ 5 }{ 3 } $ times the sides of $ABC$
Triangle $AMN$ is the required triangle.

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now

CBSE Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.1

Download the Math Ninja App Now