NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Explore the NCERT Solutions for Class 10 Maths Chapter 11: Constructions (English Medium), with detailed explanations for Exercise 11.2. This resource is designed to simplify complex Constructions problems, helping Class 10 Maths students grasp the subject effortlessly. For any queries regarding NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2, feel free to leave a comment, and we’ll respond as soon as possible.

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2
Exercise 11.2

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Download the Math Ninja App Now

1. Draw a circle of radius 6 cm . From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

Answer

Step1: Draw circle of radius 6 cm with center A, mark point C at 10 cm from center.

Step 2: find perpendicular bisector of AC

Step3: Take this point as center and draw a circle through A and C

Step 4:Mark the point where this circle intersects our circle and draw tangents through C

Length of tangents $ =8 \mathrm{~cm} $
AE is perpendicular to CE (tangent and radius relation)
In $ \triangle \mathrm{ACE} $
AC becomes hypotenuse
$\mathrm{AC}^{2}=\mathrm{CE}^{2}+\mathrm{AE}^{2}$
$10^{2}=\mathrm{CE}^{2}+6^{2}$
$\mathrm{CE}^{2}=100-36$
$\mathrm{CE}^{2}=64$
$\mathrm{CE}=8 \mathrm{~cm}$

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Download the Math Ninja App Now

2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

Answer

Steps of construction:
i. Draw two concentric circles with radii 4 cm and 6 cm respectively.

Radius $ =6 \mathrm{~cm} $
Radius $ =4 \mathrm{~cm} $
ii. Now, draw the radius OP of the larger circle.

Radius $ =6 \mathrm{~cm} $
Radius $ =4 \mathrm{~cm} $
iii. Construct a perpendicular bisector of OP intersecting OP at point $O^{\prime}$.
iv. Considering $O^{\prime}P$ as radius, draw another circle.
v. From point $ P $, draw tangents $ P Q $ and $ P R $ (can see in the figure)

Justification: By applying Pythagoras theorem, we have;
$\mathrm{PQ}^{2}=\mathrm{OP}^{2}-\mathrm{OQ}^{2}$
$=6^{2}-4^{2}$
$=36-16=20$
$ \mathrm{Or}, \mathrm{PQ}=2 \sqrt{5} \mathrm{~cm} $

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Download the Math Ninja App Now

3. Draw a circle of radius 3 cm . Take two points $ P $ and $ Q $ on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q .

Answer

Steps of construction:
i. At first draw a circle with radius 3 cm .

ii. Now, extend the diameter to A and B on both the sides.

iii. Then, draw the perpendicular bisectors of OA and OB .

Such that:
Perpendicular bisector of OA intersects it at point $ \mathrm{O}^{\prime} $.
And,
Perpendicular bisector of OB intersects it at point $O^{\prime\prime}$.

iv. Considering $O^{\prime}a$ as radius, construct another circle.
v. Considering $O^{\prime\prime}B$ as radius, construct the third circle.
vi. From point $ A $, draw tangents $ A P $ and $ A Q $.
vii. From point B, draw tangents BR and BS.

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Download the Math Ninja App Now

4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of $ 60^{\circ} $.

Answer

Steps of construction:
1) Draw a circle of radius 5 cm , and draw a radius OA anywhere in the circle.

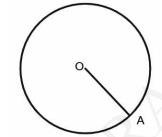
2) Taking OA as base, draw an angle AOB such that $ \angle \mathrm{AOB}=120^{\circ} $.

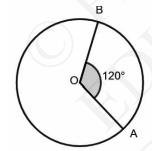
3) At $ A $, Draw a line $ A X $ such that $ A X \perp O A $.

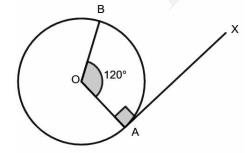
4) At $ B $, Draw a line $ B Y $ such that $ B Y \perp O B $.

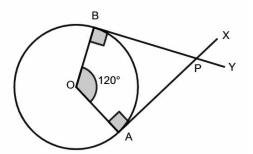
5) AX and BY intersect at P; AP and BP are required tangents.
Justification:
1) Clearly, AP and BP are tangents since tangent at a point on the circle is perpendicular to the radius through point of contact.
2) In Quadrilateral OAPB, we have $ \angle \mathrm{OAP}+\angle \mathrm{APB}+\angle \mathrm{OBP}+ $ $ \angle \mathrm{AOB}=360^{\circ} \quad $ [By Angle Sum Property]
$ \Rightarrow \angle \mathrm{OAP}+90^{\circ}+90^{\circ}+ $ $ 120^{\circ}=360^{\circ} \Rightarrow \angle \mathrm{OAP}=60^{\circ} $.

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Download the Math Ninja App Now

$Mathninja.in$

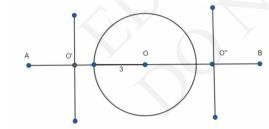
5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

Answer

Steps of construction:
i. At first, draw a line segment, $ \mathrm{AB}=8 \mathrm{~cm} $.

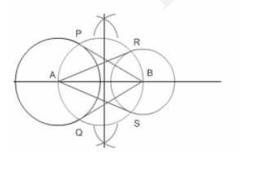
ii. Considering A as centre, construct a circle of radius 4 cm.
iii. Considering B as centre, draw another circle with radius 3 cm.
iv. Draw perpendicular bisector of AB.
v. Now, considering midpoint of AB as centre and AB as diameter, draw the third circle.
vi. From point A, draw tangents AR and AS.
vii. Then, from point B, draw tangents BP and BQ .

6. Let ABC be a right triangle in which $ \mathrm{AB}=6 \mathrm{~cm}, \mathrm{BC}=8 \mathrm{~cm} $ and $ \angle \mathrm{B}=90^{\circ} $. BD is theperpendicular from B on AC. The circle through $ \mathrm{B}, \mathrm{C}, \mathrm{D} $ is drawn. Construct the tangents from A to this circle.

Answer

Steps of construction:
i. Draw a line segment $ \mathrm{AB}=6 \mathrm{~cm} $.
ii. Draw a right angle $ \angle \mathrm{ABC} $ at point B, such that $ \mathrm{BC}=8 \mathrm{~cm} $.

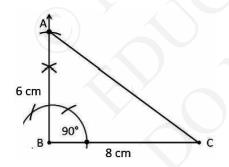
iii. Now, draw a perpendicular bisector of BC which will intersect it at P.

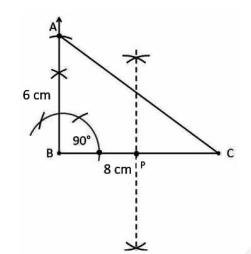
iv. Now P is a mid point of BC. Taking P as a centre and BP as radius draw a circle.

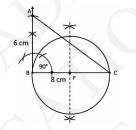
v. Join A to the centre of circle i.e. P Make perpendicular bisector of AP. Let $ Q $ be the mid point of $ A P $.

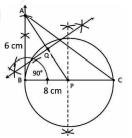
vi. Taking Q as centre and AQ as a radius draw a circle.

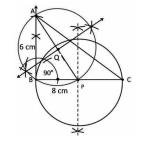
vii. Now Both circles intersect each other at B and R. Join AR.

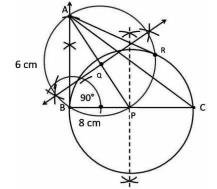
Hence $ A B $ and $ A R $ are the required tangents.
Justification:
We need to prove $ A B $ and $ A R $ are tangents.
Construction: Join PR.

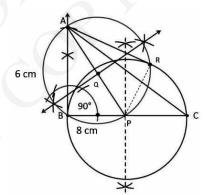
As ARP is an angle on the semicircle BPR. And angles in semicircles are of $ 90^{\circ} \therefore \angle \mathrm{ARP}=90^{\circ} \Rightarrow \mathrm{AR} \perp \mathrm{PR} $
And PR is the radius of circle, From the theorem which states that tangent is perpendicular to the radius. So AR has to be tangent. Similarly AB is a tangent. Hence proved.

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

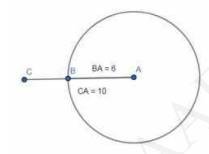
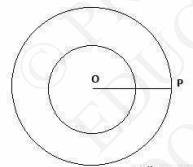
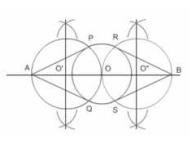
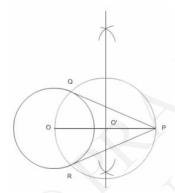
Download the Math Ninja App Now

7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.

Answer

Steps of construction:
[We will take a bangle of some fixed radius, say it is $ \mathrm{6 c m} $ ]
i. So at first draw a circle with the help of a bangle having a certain radius (say 6 cm ) and centre O.
ii. Take a point P outside the circle.
iii. Draw a line segment $ O P=10 \mathrm{~cm} $
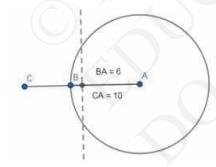
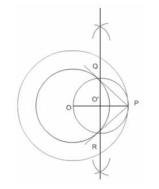
iv. Make perpendicular bisector of OP which intersects OP at point $O^{\prime}$.
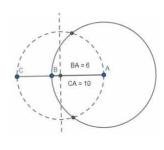
v. Take $O^{\prime}P$ as radius and draw another circle.
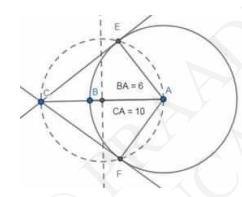
vi. From point P, draw tangents to points of intersection between the two circles.

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Download the Math Ninja App Now

NCERT Solutions for Class 10 Maths Chapter 11: Constructions || CBSE Class 10 Maths Chapter 11 Constructions solutions Ex 11.2

Download the Math Ninja App Now