NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Discover the complete NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes solutions (English Medium), with step-by-step explanations for Exercise 13.5. This resource ensures a thorough understanding of Surface Areas and Volumes, helping Class 10 Maths students excel in their exams. If you have any queries regarding the NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes solutions Ex 13.5, drop a comment below, and we’ll assist you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5
Exercise 13.5

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

1. A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be $ 8.88 \mathrm{~g} \mathrm{~per} \mathrm{~cm}^{3} $

Answer

We know that,
No. of rounds $ =\frac{\text { Height }}{\text { Diameter }} $
$=\frac{12}{0.3}=40 \text { rounds }$
Length of wire required in 1 round $ = $ Circumference of base of cylinder
$=2 \pi r$
$=2 \pi \times 5$
$=10 \pi$
Length of wire in 40 rounds $ =40 \times 10 \pi $
$=\frac{400 \times 22}{7}$
$=\frac{8800}{7}=12.57 \mathrm{~cm}$
Radius of wire $ =\frac{0.3}{2}=0.15 \mathrm{~cm} $
$\text {Volume of wire}=\text {Area of cross-section of wire} \times \text {Length of wire }$
$=\pi(0.15)^{2} \times 1257.14$
$=88.898 \mathrm{~cm}^{3}$
$\text { Mass }=\text { Volume } \times \text { Density }$
$=88.898 \times 8.88$
$=789.41 \ \mathrm{gm}$

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

2. A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose the value of $ \pi $ as found appropriate)

Answer

Let ABC be the triangle, with $ \mathrm{AB}=3 \ \mathrm{cm} \ \mathrm{BC}=4 $ cmand is revolved around hypotenuse. By Pythagoras theorem, Hypotenuse,
$\mathrm{AC}=\sqrt{3 \times 3+4 \times 4}$
$=5 \mathrm{~cm}$
Area of $ \triangle \mathrm{ABC}=\frac{1}{2} \times \mathrm{AB} \times \mathrm{BC} $
$\frac{1}{2} \times \mathrm{AC} \times \mathrm{OB}=\frac{1}{2} \times 3 \times 4$
$\mathrm{OB}=\frac{12}{5}=2.4 \mathrm{~cm}$
Volume of double cone $ = $ Volume of cone $ 1+ $ Volume of cone $2$
$=\frac{1}{3} \pi \mathrm{r}^{2} \mathrm{~h}_{1}+\frac{1}{2} \pi \mathrm{r}^{2} \mathrm{~h}_{2}$
$=\frac{1}{3} \pi \mathrm{r}^{2}\left(\mathrm{~h}_{1}+\mathrm{h}_{2}\right)$
$=\frac{1}{3} \pi \mathrm{r}^{2}(\mathrm{OA}+\mathrm{OC})$
$=\frac{1}{3} \times 3.14 \times(2.4)^{2}(5)$
$=30.14 \mathrm{~cm}^{3}$
Surface area of double cone $ = $ Surface area of cone $ 1+ $ Surface area of cone 2
$=\pi r l_{1}+\pi r l_{2}$
$l_{1}=\mathrm{AB}=3 \mathrm{~cm}$
$l_{2}=\mathrm{BC}=4 \mathrm{~cm}$
$=\pi \mathrm{r}[3+4]$
$=3.14 \times 2.4 \times 7$
$=52.75 \mathrm{~cm}^{2}$

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

3. A cistern, internally measuring $ 150 \mathrm{~cm} \times 120 \mathrm{~cm} \times 110 \mathrm{~cm} $, has $ 129600 \mathrm{~cm}^{3} $ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being $ 22.5 \mathrm{~cm} \times 7.5 \mathrm{~cm} \times 6.5 \mathrm{~cm} $ ?

Answer

According to the question:
Volume of cistern $ =150 \times 120 \times 110 $
[Volume of cube $ =\mathrm{lbh} $ where $ \mathrm{l}, \mathrm{b} $ and h are length, breadth and height respectively]
$=1980000 \mathrm{~cm}^{3}$
Volume to be filled in cistern $ =1980000-129600 $
$=1850400 \mathrm{~cm}^{3}$
Let $ n $ numbers of porous bricks were placed in the cistern
Volume of $ n $ bricks $ =n \times 22.5 \times 7.5 \times 6.5 $
$=1096.875 n$
As each brick absorbs one-seventeenth of its volume, therefore, volume absorbed by these bricks $ =\frac{n}{17}(1096.875) $
$1850400+\frac{n}{17}(1096.875)=(1096.875) n$
$1850400=\frac{16 n}{17}(1096.875)$
$\mathrm{n}=1792.41$

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

4. In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is $ 7280 \mathrm{~km}^{2} $, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.

Answer

Area of the valley $ =7280 \mathrm{~km}^{2} $
If there was a rainfall of 10 cm in the valley then amount of rainfall in the valley $ = $ area of the valley $ \times 10 \mathrm{~cm} $
Amount of rainfall in the valley $ =7280 \mathrm{~km}^{2} \times 10 \mathrm{~cm} $
[As $ 1 \mathrm{~km}=1000 \mathrm{~m}=100000 \mathrm{~cm} $]
$ 1 \mathrm{~cm}=\frac{1}{100000} \mathrm{~km} $
Amount of rainfall in one day
$ =7280 \mathrm{~km}^{2}\left(\frac{10}{100000} \mathrm{~km}\right) $
$ =0.728 \mathrm{~km}^{3} $ $ \qquad $ $\dots\dots$ [i]
Length of each river, $ l=1072 \mathrm{~km} $
The breadth of each river, $ b=75 \mathrm{~m} $
$=\frac{75}{1000} \mathrm{~km}$
Depth of each river, $ h=3 \mathrm{~m} $
$=\frac{3}{1000} \mathrm{~km}$
The volume of each river $ =l \times b \times h $
$=1072 \times \frac{75}{1000} \times \frac{3}{1000}$
$=\frac{241200}{1000000}$
$=0.2412 \mathrm{~km}^{3}$
Volume of three such rivers $ =3 \times $ Volume of each river $ =3 \times 0.2412 \mathrm{~km}^{3} $
$ =0.7236 \mathrm{~km}^{3} $ $ \qquad $ $\dots\dots$ [ii]
[i] and [ii] are approximately equal.

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

$Mathninja.in$

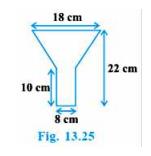
5. An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see Fig. 13.25)

Answer

Given:
Radius $ \left(r_{1}\right) $ of upper circular end of frustum part $ =\frac{18}{2}=9 \mathrm{~cm} $
Radius $ \left(r_{2}\right) $ of lower circular end of frustum part $ = $ Radius of circular end of cylindricalpart $ =\frac{8}{2}=4 \mathrm{~cm} $
Height $ \left(h_{1}\right) $ of frustum part $ =22-10=12 \mathrm{~cm} $
Height $ \left(h_{2}\right) $ of cylindrical part $ =10 \mathrm{~cm} $
Slant height $ (l) $ of frustum part
$=\sqrt{(9-4) \times(9-4)+(12) \times 12}$
$=13 \mathrm{~cm}$
Area of tin sheet required $ =\mathrm{CSA} $ of frustum part $+$ CSA of cylindrical part
$=\pi\left(r_{1}+r_{2}\right) \times l+2 \pi r_{2} \mathrm{~h}_{2}$
$=\frac{22}{7}(9+4) \times 13+2 \times \frac{22}{7} \times 4 \times 10$
$=\frac{22}{7}[169+80]$
$=\frac{22 \times 249}{7}$
$=782 \frac{4}{7} \mathrm{~cm}^{2}$

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

6. Derive the formula for the curved surface area and total surface area of the frustum of acone, given to you in Section 13.5, using the symbols as explained.

Answer

Let ABC be a cone. A frustum DECB is cut by a plane parallel to its base. Let $ r_{1} $ and $ r_{2} $ be the radii of the ends of the frustum of the cone and $ h $ be the height of the frustum of the cone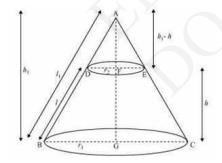

In $ \triangle \mathrm{ABG} $ and $ \triangle \mathrm{ADF}, \mathrm{DF} \| \mathrm{BG} $
$\frac{D F}{B G}=\frac{A F}{A G}=\frac{A D}{A B}$
$\frac{r_{2}}{r_{1}}=\frac{h_{1}-h}{h_{1}}=\frac{l_{1}-l}{l_{1}}$
$\frac{r_{2}}{r_{1}}=1-\frac{h}{h_{1}}=1-\frac{l}{l_{1}}$
$1-\frac{l}{l_{1}}=\frac{r_{2}}{r_{1}}$
$\frac{l}{l_{1}}=1-\frac{r_{2}}{r_{1}}=\frac{r_{1}-r_{2}}{r_{1}}$
$\frac{l_{1}}{l}=\frac{r_{1}}{r_{1}-r_{2}}$
$l_{1}=\frac{r_{1} l}{r_{1}-r_{2}}$
CSA of frustum $ \mathrm{DECB}=\mathrm{CSA} $ of cone $ \mathrm{ABC}-\mathrm{CSA} $ cone ADE
$=\pi r_{1} l_{1}-\pi r_{2}\left(l_{1}-l\right)$
$=\pi r_{1}\left(\frac{l r_{1}}{r_{1}-r_{2}}\right)-\pi r_{2}\left[\frac{r_{1} l}{r_{1}-r_{2}}-l\right]$
$=\frac{\pi \times r_{1} \times r_{1} \times l}{r_{1}-r_{2}}-\frac{\pi \times r_{2} \times r_{2} \times l}{r_{1}-r_{2}}$
$=\pi l\left[\frac{r_{1} \times r_{1}-r_{2} \times r_{2}}{r_{1}-r_{2}}\right]$
$\mathrm{CSA}=\pi\left(\mathrm{r}_{1}+\mathrm{r}_{2}\right) \times l$
Total surface area of frustum $ = $ CSA $+$ Area of upper circular end $+$ Area of lower circular end
$=\pi\left(r_{1}+r_{2}\right) \times 1+\pi r_{2} ^{2}+\pi r_{1}^{2}$
$=\pi\left[\left(r_{1}+r_{2}\right) \times l+r _{1}^{2}+r_{2} ^{2}\right]$

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

7. Derive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.

Answer

Let ABC be a cone.
And,
A frustum DECB is cut by a plane parallel to its base
Now,
Let $ r_{1} $ and $ r_{2} $ be the radii of the ends of the frustum of the cone and $ h $ be the height of the frustum of the cone

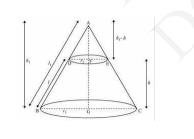
In $ \triangle \mathrm{ABG} $ and $ \triangle \mathrm{ADF}, \mathrm{DF} \| \mathrm{BG} $
$ \frac{D F}{B G}=\frac{A F}{A G}=\frac{A D}{A B}$
$\frac{r_{2}}{r_{1}}=\frac{h_{1}-h}{h_{1}}=\frac{l_{1}-l}{l_{1}}$
$\frac{r_{2}}{r_{1}}=1-\frac{h}{h_{1}}=1-\frac{l}{l_{1}}$
$\frac{1}{1-\frac{h}{h_{1}}}=\frac{r_{2}}{r_{1}}$
$\frac{h}{h_{1}}=1-\frac{r_{2}}{r_{1}}=\frac{r_{1}-r_{2}}{r_{1}}$
$\frac{h_{1}}{h}=\frac{r_{1}}{r_{1}-r_{2}}$
$h_{1}=\frac{r_{1} h}{r_{1}-r_{2}} $
Volume of frustum of cone $ = $ Volume of cone ABC $-$ Volume of cone ADE
$=\frac{1}{3} \pi \mathrm{r}_{1}^{2} \mathrm{h}_{1}-\frac{1}{3} \pi \mathrm{r} _{2}^{2}\left(\mathrm{h}_{1}-\mathrm{h}\right)$
$=\frac{\pi}{3}\left[\mathrm{r}_{1}^{2} \mathrm{h}_{1}-\mathrm{r} _{2}^{2}\left(\mathrm{h}_{1}-\mathrm{h}\right)\right]$
$=\frac{\pi}{3}\left[\mathrm{r} _{1}^{2}\left(\frac{h r_{1}}{r_{1}-r_{2}}\right)-\mathrm{r}_{2}^{2}\left(\frac{h r_{1}}{r_{1}-r_{2}}-h\right)\right]$
$=\frac{\pi}{3}\left[\frac{h \times r_{1} \times r_{1} \times r_{1}}{r_{1}-r_{2}}-\frac{h \times r_{2} \times r_{2} \times r_{2}}{r_{1}-r_{2}}\right]$
$ =\frac{\pi}{3} \times \mathrm{~h}\left[\frac{r_{1} \times r_{1} \times r_{1}-r_{2} \times r_{2} \times r_{2}}{r_{1}-r_{2}}\right] $
$=\frac{\pi}{3} \mathrm{~h}\left[\frac{\left(r_{1}-r_{2}\right)\left(r_{1} \times r_{1}+r_{2} \times r_{2}+r_{1} \times r_{2}\right)}{r_{1}-r_{2}}\right]$
$=\frac{1}{3} \mathrm{~h}\left[r_{1}^{2}+r _{2}^{2}+r_{1} r_{2}\right] $

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now

NCERT Solutions for Class 10 Maths Chapter 13: Surface Areas and Volumes || CBSE Class 10 Maths Chapter 13 solutions Ex 13.5

Download the Math Ninja App Now